Après avoir traité les bases de l’acoustique et le rayonnement acoustique, cet article aborde la problématique de la production d’ondes sonores avec un haut-parleur électroacoustique. Nous nous appuierons sur ce que nous y avons appris et nous utiliserons le principe de l’induction électromagnétique ainsi qu’un peu de mécanique pour comprendre le fonctionnement d’un haut-parleur électrodynamique. Le modèle que nous dresserons nous permettra d’isoler les grandeurs physiques importantes et de discuter de l’ordre de grandeur de leurs valeurs.
- Données techniques d’un haut-parleur
- Equation mécanique
- Equation électrique
- Impédance
- Rayonnement acoustique
- Valeurs maximales
- Hautes fréquences
- Conclusion
Données techniques d’un haut-parleur
Description
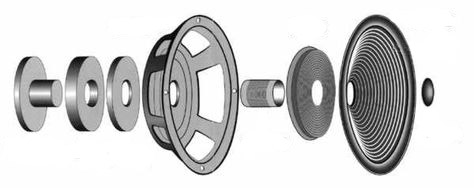
Fixons sur un aimant cylindrique entouré d’une bobine une structure rigide qu’on appelle saladier. Tendons maintenant une membrane de faible masse entre la bobine et le saladier, la fixation sur le saladier étant élastique, équivalente à un ressort.
Lorsque la bobine d’inductance vibre autour de sa position d’équilibre sous l’effet de la force de Laplace (voir plus bas) , elle entraîne dans son mouvement la membrane. Celle-ci, à son tour, fait vibrer l’air en fonction de son facteur de rayonnement.
Nous considèrerons dans tout cet article que le haut-parleur est monté sur un baffle infini (voir l’article précédent pour la description du modèle).

Jeu de paramètres
Un haut-parleur est décrit par un jeu de paramètres mécaniques et électriques appelé paramètres de Thiele et Small. Afin d’illustrer les différents résultats que nous obtiendrons, nous choisissons ici un haut-parleur grave-medium d’entrée de gamme Monacor SP-165PA de diamètre 16 cm dont nous indiquons les données catalogue.

- Surface efficace de la membrane S = 137\times10^{-4}\,\text{m}^2
- Masse de l’équipage mobile (bobine + membrane) m = 8,2\times10^{-3} \,\text{kg})
- Raideur de la suspension élastique k = 4,0\times 10^{3} \,\text{N}\,\text{m}^{-1}) (on trouve fréquemment son inverse, la compliance C = 1/k de la suspension en \text{m}\,\text{N}^{-1})
- Résistance mécanique de la suspension \alpha= 1,2 \,\text{kg}\,\text{s}^{-1} (coefficient de la vitesse dans l’expression de la force de frottement fluide)
- Résistance de la bobine R_e = 6.9\,\Omega (l’indice e se réfère aux grandeurs électriques)
- Inductance de la bobine L_e= 0,50 \times10^{-3} \,\text{H}
- Facteur de force Bl = 7,1 \,\text{T}\,\text{m} (produit du champ magnétique par la longueur de la bobine)
À quoi nous rajoutons la valeur limite du déplacement de la membrane pour laquelle la réponse est linéaire : x_\text{max} = 3,75 \times10^{-3} \,\text{m}
Equation mécanique
Force de Lorentz
Une particule chargée, de charge q, plongée dans un champ électrique \vec{E} subit la force électrique \vec{F_e}=q \cdot \vec{E}. Cette force est colinéaire au champ électrique et a même sens que lui si la particule est chargée positivement.
Une particule chargée, de charge q en mouvement à la vitesse \vec{v} est plongée dans un champ magnétique \vec{B}. Elle subit alors la force magnétique \vec{F_m}=q\vec{v} \land \vec{B}, où le symbole \land désigne le produit vectoriel. La direction résultante de \vec{F_m} est donnée par la règle de la main droite (voir figure).

En sommant ces deux forces, on obtient la force de Lorentz qui s’exerce sur une particule chargée plongée dans un champ électromagnétique :
\vec{F}=q \cdot (\,\vec{E} + \vec{v} \land \vec{B})\,
Force de Laplace exercée sur un conducteur
Soit un circuit électrique filiforme, parcouru par un courant I, en mouvement dans un champ électromagnétique (\, \vec{E},\,\vec{B} )\, à la vitesse \vec{V}.
Toutes les particules chargées du conducteur (ions métalliques et électrons libres) sont soumises à la force de Lorentz.
Pour les ions métalliques, de charge positive, e correspondant à la charge élémentaire :
\vec{F}_{ion}=e \cdot (\,\vec{E} + \vec{V} \land \vec{B})\,
Pour les électrons libres, de charge opposée en mouvement à la vitesse \vec{u} dans le circuit :
\vec{F}_{elec}=-e \cdot (\,\vec{E} + (\,\vec{V} + \vec{u})\,\land \vec{B})\,
Il y a autant d’ions métalliques que d’électrons libres. Toutes les contributions s’annulent sauf celle due à la vitesse propre des électrons dans le circuit. La force exercée globalement sur le circuit, appelée force de Laplace, est donc la somme de toutes les forces \vec{f}=-e \vec{u}\land \vec{B} exercées sur chacun des électrons libres.
Cas particulier de la bobine d’un haut-parleur
Pour simplifier la suite, plaçons-nous d’ores et déjà dans la géométrie qui nous intéresse pour l’étude du haut parleur. Le conducteur est une bobine de fil de longueur totale l plongée dans un champ magnétique radial d’intensité B :


D’après la règle de la main droite, pour un courant circulant dans le sens horaire (et donc des électrons circulant dans le sens trigonométrique) toutes les forces à sommer sont donc colinéaire à l’axe central du dispositif, dirigées suivant les x croissants. C’est la convention choisie sur les haut-parleurs : la borne teintée de rouge ou indiquée “+” correspond au sens de branchement pour lequel un courant positif met l’équipage mobile en mouvement vers l’extérieur. Il nous reste à sommer les contributions \vec{f}=-e\cdot u\cdot B \cdot \vec{e}_x pour chacun des électrons libres (\vec{e}_x est le vecteur unitaire portant l’axe x).
Combien y-a-t-il d’électrons libres dans cette bobine ? Le courant étant le débit de charges, il y a n=I/e électrons qui traversent une section du circuit en une seconde. Les derniers à la traverser sont ceux qui étaient situés à une distance \delta = u \times 1\,\text{s} une seconde auparavant. Si l est la longueur totale du fil, il y en a donc \frac{l}{\delta} fois plus : il y a en tout N = n \cdot \frac{l}{\delta}=\frac{I \cdot l}{u\cdot e} électrons libres. La force de Laplace exercée sur la bobine est finalement :
\vec{F}_L=N \cdot \vec{f}=\frac{I \cdot l}{u\cdot e} \cdot (\,-e)\,\cdot u\cdot B \cdot \vec{e}_x=I \cdot Bl \cdot \vec{e}_x
Si la bobine est parcourure par un courant d’intensité constante i, la force de Laplace exercée sur elle sera donc constante elle aussi. Mais si, maintenant, on impose un courant variable i dans la bobine, on voit que la force de Laplace sera elle aussi variable. Elle poussera la bobine tantôt à droite (lorsque le courant est positif) et tantôt à gauche (lorqu’il est négatif). L’effet sera donc de faire vibrer la bobine autour de sa position d’équilibre.
L’énergie mécanique vibratoire pourra alors être transmise en partie à l’air, comme nous l’avons détaillé dans l’article précédent.
Notons enfin que la force de Laplace est proportionnelle au facteur de force Bl affiché par les constructeurs.
Principe fondamental de la dynamique
Appliquons le principe fondamental de la dynamique au système {bobine + membrane} de masse m dans le référentiel de l’aimant : m \cdot \vec{a} = \Sigma\, \vec{F}_\text{ext}.
Les forces exercées suivant l’axe x sont :
- la force de rappel -k\cdot x due à la fixation élastique, qui ramène le système vers sa position d’équilibre ;
- une force dissipative de frottements fluides proportionnelle à la vitesse du système -\alpha \cdot v_x = -\alpha \cdot \dot{x} ;
- la force de Laplace Bl \cdot i exercée sur la bobine ;
- les forces de pression -p_\text{avant} S et p_\text{arrière} S dues à la pression de l’air sur les faces de la membrane. Ces forces caractérisent le rayonnement acoustique du haut-parleur.
Nous avons vu que les forces de pression pouvaient s’écrire : Z_\text{R} \cdot \dot{x}, avec Z_\text{R} = R_\text{R} + j \omega m_\text{R} l’impédance de rayonnement. Les expressions de la résistance de rayonnement R_\text{R} et de la masse de rayonnement m_\text{R} sont, pour un piston encastré dans un plan infini, dans l’approximation des basses fréquences :
\displaystyle{ R_\text{R} \approx \rho c S \sigma = \frac{\rho_0 S^2 }{2\pi c}\omega^2 \hspace{1cm}\text{et} \hspace{1cm} m_\text{R} \approx \frac{8\rho}{3}\left(\frac{S}{\pi}\right)^{3/2} }
Pour le haut-parleur Monacor pris en exemple, on obtient :
\displaystyle{ R_\text{R} \approx 1,0\times10^{-7}\omega^2 \;\text{kg}\,\text{s}^{-1}\hspace{1cm}\text{et} \hspace{1cm} m_\text{R} \approx 0,9 \,\text{g} }
La résistance de rayonnement est donc négligeable devant la résistance mécanique jusqu’à \omega \approx 10^3 \,\text{rad}\,\text{s}^{-1}. L’expression utilisée n’est de toute manière valable qu’aux basses fréquences. La masse de rayonnement quant à elle implique une faible correction de l’ordre de quelques pourcents.
Contrairement au modèle du piston solide, la membrane du haut-parleur est en contact avec l’air des deux côtés du baffle : masse de rayonnement et résistance de rayonnement sont à prendre en compte pour le rayonnement avant et pour le rayonnement arrière.
On obtient donc l’équation différentielle relative à la position de la bobine (équation mécanique du haut-parleur) :
(m + 2m_\text{R}) \cdot \ddot{x} = -k \cdot x - (\alpha + 2R_\text{R})\cdot \dot{x} + Bl \cdot i
Equation électrique
Force électromotrice induite
Lorsqu’un circuit est mobile dans un champ magnétique, la force magnétique exercée sur les électrons libres va les mettre en mouvement. Un courant induit apparaît donc spontanément dans le circuit. On appelle force électromotrice u_\text{ind} la différence de potentiel expliquant l’apparition de ce courant électrique. Nous établirons dans ce paragraphe l’expression de la f.e.m. induite dans la bobine d’un haut parleur en mouvement dans le champ magnétique de l’aimant.
Dans le référentiel de l’aimant, il règne dans l’entrefer un champ magnétique \vec{B} radial. Lorsque la bobine est en mouvement à la vitesse \vec{V}, les électrons libres subissent une force de Lorentz \vec{F}=-e \cdot \vec{V} \land \vec{B}. D’après la règle de la main droite, cette force aura tendance à mettre les électrons en mouvement dans le sens trigonométrique, et donc à générer un courant positif dans la bobine. En appelant \vec{u} le vecteur unitaire dirigé en chaque point de la bobine dans le sens d’une intensité positive : \vec{F}= e \cdot V \cdot B \cdot \vec{u}.
Plaçons nous maintenant dans le référentiel de la bobine. On vient de voir que des électrons initialement immobiles se mettront en mouvement dans le sens horaire. Ils sont donc soumis à l’effet d’un champ électrique \vec{E}' qui s’écrit, par définition :
\displaystyle{ \vec{E}' = \frac{\vec{F}}{q} = \frac{e \cdot V \cdot B \cdot \vec{u}}{-e}= V \cdot B \cdot \vec{u} }
La force électromotrice induite est égale à la circulation du champ électrique entre les deux extrémités de la bobine ;
u_\text{ind}= \int_0^l \vec{E}' \cdot \text d \vec{l} =- V \cdot Bl
Loi des mailles
La loi des mailles donne :
u(t)\, + u_\text{ind}(t)\, = u_R + u_L \, \iff \, R \cdot i + L \cdot \frac{\text{d}i}{\text{dt}} = u(t)\, - Bl \cdot \dot{x}
Cette équation est appelée équation électrique du haut-parleur. Elle est donc, sans surprise, l’équation d’un circuit R,L en régime forcé. Mais la tension forçant le circuit contient deux termes : la tension imposée et la f.e.m. due à la vitesse de la bobine.
Impédance
Solution en régime sinusoïdal forcé
Nous avons vu que la résistance de rayonnement est faible devant le coefficient de frottement mécanique : R_\text{R} \ll \alpha. Nous négligerons donc le terme contenant R_\text{R} dans cette section qui ne traite que du comportement électrique du haut-parleur.
Un haut-parleur est donc régi par deux équations :
\left\{ \begin{array}{ll} (m + 2m_\text{R})\cdot \ddot{x} + \alpha \cdot \dot{x} + k \cdot x = Bl \cdot i \\ R \cdot i + L \cdot \frac{\text{d}i}{\text{dt}} = u(\,t)\, - Bl\cdot \dot{x} \end{array}\right.
Ces deux équations sont couplées, puisque l’équation mécanique contient la variable électrique i et que l’équation électrique contient la variable mécanique x. Les coefficients de couplage sont respectivement Bl et - Bl : ils sont opposés.
Recherchons des solutions particulières de ces équations en imposant un régime sinusoïdal. Un son plus complexe sera décrit par un ensemble de fréquences, et donc par une somme de sinusoïdes, comme expliqué ici. Imposons donc dans l’équation mécanique une intensité sinusoïdale \underline{i}=\underline{I} \cdot \exp{(\,j \omega t)\,}. Nous utilisons ici la notation complexe.
Injectons maintenant dans l’équation une solution sinusoïdale pour x, c’est à dire une solution s’écrivant sous la forme \underline{x}=\underline{X} \cdot \exp{(\,j \omega t)\,}. On obtient :
\left[(m + 2m_\text{R}) (j \omega)^2 + j \omega \alpha + k \right] \cdot \underline{X} = Bl \cdot \underline{I}
En opérant de la même manière pour l’équation électrique :
\underline{U} - Bl \cdot \underline{\dot{X}}= \left( R + j \omega L \right) \underline{I}
Eliminons \underline{X} de la deuxième équation en utilisant la première :
\displaystyle{\underline{\dot{X}} = \frac{ j \omega \cdot Bl}{(m + 2m_\text{R}) (j\omega)^2 +j \omega \alpha + k} \cdot \underline{I}}
\displaystyle{\underline{U} = \left( R + j \omega L + \frac{j \cdot \omega \cdot (Bl)^2}{(m + 2m_\text{R}) (j\omega) ^2 +j \omega \alpha + k}\right)\underline{I}}
Où l’impédance électrique du haut-parleur \underline{Z} = \underline{U} / \underline{I} apparaît :
\displaystyle{\underline{Z} = R + j \omega L + \frac{j \omega \cdot (Bl)^2}{(m + 2m_\text{R}) (j\omega)^2 -j \omega \alpha + k} }
Le terme R + j \omega L est l’impédance électrique classique d’une bobine, le deuxième terme est dû au mouvement de la bobine dans le champ magnétique de l’aimant et est appelé impédance motionnelle :
\displaystyle{\underline{Z}_{\text{mot}} = \frac{j \omega \cdot l^2 \cdot B^2}{(m + 2m_\text{R}) \omega ^2 -j \omega \alpha - k} }
Circuit électrique équivalent
Remarquons maintenant que l’impédance motionnelle peut s’écrire :
\displaystyle{\underline{Z}_{\text{mot}} = \frac{1}{\frac{j \omega (m + 2m_\text{R})}{(Bl)^2} + \frac{\alpha}{(Bl)^2} +\frac{k}{j \omega (Bl)^2}} }
Soit :
\displaystyle{\frac{1}{\underline{Z}_{\text{mot}}} = \frac{1}{j \omega L_\text{mot}}+ \frac{1}{R_\text{mot}} + \frac{1}{\frac{1}{j\omega C_\text{mot}} } }
avec
\displaystyle{\left\{ \begin{array}{ll} L_{\text{mot}} = \frac{m + 2m_\text{R}}{(Bl)^2}\\ R_{\text{mot}} = \frac{(Bl)^2}{\alpha} \\ C_{\text{mot}} = \frac{(Bl)^2}{k} \end{array}\right.}
On reconnait ainsi l’association en parallèle d’un condensateur de capacité C_{\text{mot}}, d’un résistor de résistance R_{\text{mot}} et d’une bobine d’inductance L_{\text{mot}}.
Pour le haut-parleur utilisé en exemple, on obtient :
- C_{\text{mot}} = 198 \,\text{µF}
- R_\text{mot} = 42,0 \,\Omega
- L_\text{mot}= 12,6 \,\text{mH}
Prenons un instant pour comprendre l’origine physique de ces trois effets. La masse en mouvement permet le stockage d’énergie (du fait de l’inertie) comme une bobine stocke de l’énergie magnétique lorsque des charges la traversent. Les forces de frottement dissipent de l’énergie comme le fait une résistance par effet Joule. Enfin, la raideur du ressort permet, par la force de rappel, le stockage d’énergie élastique, comme un condensateur stocke de l’énergie électrique par accumulation de charges.
Le schéma électrique équivalent d’un haut-parleur est finalement :

La résonance du circuit motionnel R_{\text{mot}}, \, L_{\text{mot}} , \, C_{\text{mot}} en parallèle se produit à la pulsation
\displaystyle{\left( \frac{\text{d}\underline{Z}_\text{mot}}{\text{d}\omega}\right)_{\omega=\omega_0} = 0 \iff \omega_0 = \frac{1}{\sqrt{L_{\text{mot}} \cdot C_{\text{mot}}}} = \sqrt{\frac{k}{m + 2m_\text{R}}}}.

Dans notre exemple, \omega_0 = 606\,\text{rad}\,\text{s}^{-1} soit f_0 = 96\,\text{Hz}. Le pic du module d’impédance est |\underline{Z}|_\text{max}=R_e+R_\text{mot}=49\,\Omega.
Deux faits importants à noter ici :
- Le pic d’impédance à la fréquence de résonance f_0 = \frac{\omega_0}{2\pi} implique que le haut-parleur ne peut pas générer de son de fréquence inférieure. Cette fréquence constitue donc la limite basse de la bande passante. En effet, bien que commercialisé en affichant sa puissance, un amplificateur est bien un amplificateur de tension. Or la puissance est \mathcal{P} = \frac{U^2}{|\underline{Z}|}: elle s’effondre en s’approchant du pic d’impédance.
- Aux basses fréquences, l’impédance électrique du haut parleur est quasiment résistive : \underline{Z}_{e} = R_e + j\omega L_e \approx R_e. Mais lorsque la pulsation s’approche de la valeur \omega = R_e/L_e (dans notre exemple proche de 14 000 \,\text{rad}\,\text{s}^{-1}), les effets inductifs commencent à apparaître et l’impédance remonte.
- Entre ces deux valeurs, le module de l’impédance passe par un minimum Z, qui est l’impédance affichée par le constructeur.
Seules les performances acoustiques d’un haut-parleur sont, in fine, d’intérêt. L’étude électrique a cependant d’intéressant que la mesure de la courbe d’impédance, plus simple à réaliser avec précision qu’une mesure acoustique, permet de déterminer certaines caractéristiques acoustiques du haut-parleur (résistance motionnelle, pulsation de résonance).
Rayonnement acoustique
Circuit acoustique équivalent
Repartons maintenant de l’équation mécanique et de l’équation électrique et éliminons le courant de l’équation mécanique. On obtient sans difficulté :
\displaystyle{\frac{Bl\cdot\underline{U}}{R_e+j\omega L_e} = \left[ j\omega (m+2m_\text{R}) + (\alpha + 2R_\text{R}) + \frac{k}{j\omega} + \frac{(Bl)^2}{R_e + j\omega L_e} \right] \cdot \underline{\dot{X}} }
Il s’agit d’une égalité entre termes de la dimension d’une force, soit une énergie par unité de longueur. En divisant par la surface du haut-parleur S, on obtient donc une égalité entre pressions (le Pascal est une énergie par unité de volume):
\displaystyle{ \frac{(Bl)\cdot\underline{U}}{S(R_e+j\omega L_e)} = \left[ \frac{ j\omega (m+2m_\text{R})}{S^2} + \frac{\alpha + 2R_\text{R}}{S^2} + \frac{k}{j\omega S^2} + \frac{(Bl)^2}{S^2(R_e + j\omega L_e)} \right] \cdot \underline{Q}}où \underline{q} = S \cdot \dot{\underline{x}} = \underline{Q} \exp{(j \omega t)} est le débit du haut-parleur.
Aux basses-fréquences (\omega \ll R_e/L_e), le terme de gauche est indépendant de la fréquence:
\displaystyle{ \frac{(Bl)\cdot\underline{U}}{S\cdot R_e} = \left[ j\omega \frac{m + 2m_\text{R}}{S^2} + \frac{\alpha + 2R_\text{R}}{S^2} + \frac{1}{j\omega} \frac{k}{S^2} + \frac{(Bl)^2}{S^2\cdot R_e} \right] \cdot \underline{Q}}On obtient alors une équation “électrique” décrivant une association en série de quatre résistances, un condensateur et une bobine :
\displaystyle{ \underline{P}_g = \left(R_{ae} + R_{as} + \frac{1}{j\omega \, C_{as}} + j\omega M_{as}+R_{ar,1}+R_{ar,2} \right) \cdot \underline{Q}}
Avec :
- L’équivalent de la tension est la pression excitatrice \underline{p}_g=\underline{P}_g \exp (j\omega t) avec \underline{P}_g = \frac{(Bl)\cdot\underline{U}}{S\cdot R_e}, exprimée en Pascals.
- Le courant correspondant est le débit \underline{q} = \underline{Q} \exp (j\omega t), en \text{m}^3/\text{s}
- Les résistances acoustiques sont, en \text{Pa}\cdot\text{s}/\text{m}^3:
- R_{ae}=\frac{(Bl)^2}{S^2 R_e} (pertes électriques dans la bobine)
- R_{as}=\frac{\alpha}{S^2} (pertes par frottements)
- La compliance acoustique (équivalent d’une capacité) est, en \text{m}^3/\text{Pa} : C_{as}=\frac{S^2}{k}. La compliance, très utilisée en acoustique, est l’inverse de la raideur.
- La masse acoustique (équivalent d’une inductance) est, en \text{kg}/\text{m}^4 : M_{as}=\frac{m + 2m_\text{R}}{S^2}
- Les résistances acoustiques de rayonnement avant R_{ar,1}=\frac{R_\text{R}}{S^2} et arrière R_{ar,2}= R_{ar,1}
L’indice s suivant l’indice “acoustique” a correspond au haut-parleur (speaker) seul. Nous le changerons pour un b (box) lorsqu’il sera encastré dans un caisson et que les grandeurs correspondantes en seront modifiées.
On peut maintenant résoudre le problème physique par analogie avec un circuit électrique. Le circuit équivalent est le suivant :

Débit acoustique
Nous pouvons ici aussi, compte tenu du faible rendement des haut-parleurs,négliger les résistances de rayonnement dans le calcul du débit du haut-parleur. La fonction de transfert du haut-parleur s’écrit alors :
\displaystyle{ \underline{Q} = \frac{1}{R_{ae} + R_{as} + \frac{1}{j\omega \, C_{as}} + j\omega M_{as}}\cdot \underline{P}_g }
\displaystyle{ \iff \underline{Q} = \frac{1}{( j\omega)^2 C_{as} M_{as} + j \omega C_{as}R_{ae} + j \omega C_{as}R_{as} + 1} \cdot j \omega C_{as} \underline{P}_g }
C’est la fonction de transfert d’un oscillateur amorti par les termes résistifs, qui se comporte donc comme un filtre passe-bande. Sa pulsation de résonance est : \omega_s^2 = 1/(C_{as}M_{as}) = k/(m + 2m_\text{R}) = \omega_0^2. La résonance du débit a donc lieu a la fréquence correspondant au pic d’impédance électrique.
Posons :
- \nu = \omega / \omega_s la pulsation réduite ;
- Q_{es} =\frac{1}{\omega_s C_{as}R_{ae}} le facteur de qualité électrique (pour le Monacor étudié Q_{es} = 1,11) ;
- Q_{ms} =\frac{1}{\omega_s C_{as}R_{as}} le facteur de qualité mécanique (pour le Monacor : Q_{ms}= 5,0).
L’expression du débit devient :
\displaystyle{ \underline{Q} = \frac{j\nu}{( j\nu)^2 + j\nu \left(\frac{1}{Q_{es}}+ \frac{1}{Q_{ms}}\right) + 1} \cdot \omega_s C_{as} \underline{P}_g }
Posons enfin Q_{ts} le facteur de qualité total tel que \frac{1}{Q_{ts}} = \frac{1}{Q_{es}} + \frac{1}{Q_{ms}} (pour l’exemple, on a Q_{ts} = 0,91 ):
\displaystyle{\boxed{ \underline{Q} = \frac{j\nu}{( j\nu)^2 +\frac{j\nu}{Q_{ts}} + 1} \cdot \omega_s C_{as} \underline{P}_g }}Puissance rayonnée
On sait que :
\displaystyle{ \mathcal{P}_{ar} = R_\text{R} V_\text{eff}^2 = \frac{R_\text{R}}{S^2} Q_\text{eff}^2 = \frac{R_\text{R}}{2 S^2} |Q|^2}
Par ailleurs R_\text{R} = \rho_0 c S \sigma. Il vient :
\displaystyle{ \mathcal{P}_{ar} = \frac{\rho_0 c \sigma}{2 S} |Q|^2}
Nous sommes ici en approximation basse fréquence vis à vis des caractéristiques du haut-parleur (\omega \ll \frac{R_e}{L_e}). Les basses fréquences vis à vis des caractéristiques acoustiques sont définies par ka \ll 1 \iff \omega \ll \frac{c}{a} (a étant le rayon du haut-parleur).
Pour notre exemple, on a a = \sqrt{S/\pi} = 0,066 \, \text{m} : \omega \ll \frac{c}{a} \approx 5 000 \, \text{rad}\cdot \text s ^{-1} \approx 800 \, \text{Hz}
Ces deux approximations sont donc du même ordre de grandeur. Dans leur respect ( f < 300 \, \text{Hz}), le facteur de rayonnement du haut parleur bafflé est bien, comme on l’a déjà utilisé plus haut, \sigma \approx \frac{a^2 k^2}{2} = \frac{S}{2\pi c^2}\omega^2. Il vient :
\displaystyle{ \mathcal{P}_{ar} = \frac{\rho_0 }{4\pi c}\omega^2|Q|^2 }
La courbe de réponse du haut-parleur en basse fréquence est alors, en injectant l’expression de l’amplitude du débit :
\displaystyle{ \boxed{ \mathcal{P}_{ar} = \frac{\rho_0 \left( \omega_s^2 C_{as} \underline{P}_g \right) ^2}{4\pi c} \left|\underline{H}_P\right|^2} \hspace{1cm} \text{avec} \hspace{1cm} \boxed{\underline{H}_P = \frac{\nu^2}{( j\nu)^2 +\frac{j\nu}{Q_{ts}} + 1} }}
Sous la forme a+jb, la fonction de transfert s’écrit :
\displaystyle{ \underline{H}_P = \frac{ \displaystyle{\frac{\nu^3}{Q_{ts}}}+j \nu^2 (1-\nu^2)} {\nu^4 + \nu^2 \left(-2 + \displaystyle{\frac{1}{Q_{ts}^2}} \right) + 1} }
Le carré de son module est :
\displaystyle{ |\underline{H}_P|^2 = \frac{\nu^4} {\nu^4 + \nu^2 \left(-2 + \displaystyle{\frac{1}{Q_{ts}^2}} \right) + 1} }
À basse fréquence \nu \rightarrow 0, un développement limité donne : |\underline{H}_P|^2 \approx \nu^4. Le comportement asymptotique du niveau sonore est donc une droite de pente 12 dB/octave (la puissance est en effet multipliée par 2^4=16 lorsque la fréquence double).
L’allure du carré du module de la fonction de transfert est la suivante :

On voit sur l’expression précédente qu’il n’y aura de résonance (courbes rouge et violette ci-dessus) que si -2 + \frac{1}{Q_{ts}^2} < 0 \iff Q_{ts} > 1/\sqrt{2}. Un bon haut-parleur assurera une transition douce vers les graves et ne présentera donc pas de pic de puissance prononcé : il aura un facteur de qualité maximal Q_{ts} \leq \frac{1}{\sqrt{2}}.
La coupure à 3\,\text{dB} se produit pour |\underline{H}_P|^2 = \frac{1}{2}, soit pour :
\nu_3^2 = \left( \frac{1}{2Q_{ts}^2}-1\right) + \sqrt{1+\left( \frac{1}{2Q_{ts}^2}-1\right)^2}
En valeurs numériques :
- Q_{ts} = 0,3 \hspace{1cm} \nu_3 = 9.2
- Q_{ts} = 0,5 \hspace{1cm} \nu_3 = 2.4
- Q_{ts} = 0,7 \hspace{1cm} \nu_3 = 1,0
- Q_{ts} = 0,9 \hspace{1cm} \nu_3 = 0,7
- Q_{ts} = 1,2 \hspace{1cm} \nu_3 = 0,6
Pour qu’il assure aussi une puissance maximale jusqu’à la coupure (au contraire des courbes bleue et orange qui s’effondrent tôt), un bon haut parleur aura donc un facteur de qualité total proche de Q_{ts} \approx 1/\sqrt{2} \approx 0,7 (courbe verte).
Notre haut-parleur d’étude, de Q_{ts} \approx 0,9, est proche de la courbe rouge. Du point de vue de la coupure à -3 dB dans les basses, il est plutôt bon. De celui d’une transition douce vers le basses, ce n’est pas un excellent choix.
Rendement
Le rendement du haut-parleur est :
\displaystyle{ \eta = \frac{\mathcal{P}_{ar}}{\mathcal{P}_e} }
où \mathcal{P}_e = \frac{U_\text{eff}^2}{|\underline{Z}|} est la puissance électrique consommée par le haut-parleur. Ces grandeurs dépendant de la fréquence, le rendement sera évalué au minimum du module d’impédance, pour lequel |\underline{Z}| \approx R_e et |\underline{H}_P| = 1. Alors :
\displaystyle{ \eta_0 = \frac{\rho_0}{4\pi c} \frac{ \left(\omega_s^2 C_{as} \underline{P}_g \right) ^2}{U_\text{eff}^2/R_e} }
En développant l’expression de la pression d’excitation, il vient :
\displaystyle{ \eta_0 = \frac{\rho_0}{4\pi c} \frac{ \left(\omega_s^2 C_{as} \frac{(Bl)\sqrt{2}U_\text{eff}}{S\cdot R_e} \right) ^2}{U_\text{eff}^2/R_e} = \frac{\rho_0}{2\pi R_e c} \left( \frac{\omega_s^2 C_{as}(Bl)}{S} \right) ^2 }
Expression qui devient, en fonction uniquement de données constructeur :
\displaystyle{ \boxed{ \eta_0 = \frac{\rho_0}{2\pi R_e c} \left( \frac{S(Bl)}{m + 2m_\text{R}} \right) ^2 }}L’application numérique pour le woofer étudié donne : \eta_0 = 0,8\%.
Le rendement d’un haut-parleur est généralement inférieur à 1%, ce qui justifie d’une autre manière d’avoir négligé dans les calculs précédents la résistance de rayonnement.
Niveau sonore, sensibilité
En champ lointain, le rayonnement de la membrane est isotrope. L’intensité sonore à une distance r s’obtient donc en divisant la puissance acoustique par la surface de la demi-sphère sur laquelle se dilue l’énergie :
I = \displaystyle{ \frac{\mathcal{P}_{ar}}{2\pi r^2} = \frac{\rho_0}{8\pi^2 c}\left(\frac{\omega_s^2 C_{as} \underline{P}_g}{r} \right)^2 \left| \underline{H}_P \right|^2 }
Le niveau sonore est, par définition :
L=10\, \log \frac{I}{I_0}
La sensibilité L_1 d’un haut-parleur est le niveau sonore obtenu à une distance de r_0 = 1 \,\text{m} du haut-parleur lorsqu’il est alimenté par une tension efficace U_\text{eff}= 2,83V (qui correspond, pour une impédance de 8 \Omega, à une puissance électrique moyenne \mathcal{P}_e = U_\text{eff}^2/Z=1\,\text{W}). La sensibilité est évaluée dans la plage de fréquence où le haut-parleur est le plus efficace (|\underline{H}_P| = 1).
On peut écrire, avec cette définition :
\displaystyle{ L_1=10\, \log \frac{\eta_0 U_\text{eff}^2 / (2\pi R_e)}{I_0}=10\, \log \frac{ U_\text{eff}^2}{2\pi I_0} + 10\, \log \frac{\eta_0}{R_e} = 121,1 + 10\, \log \frac{\eta_0}{R_e} }
Cette relation donne, appliquée au woofer : L_1 = 91,5\,\text{dB}.
Déplacement de la membrane
L’excursion de la membrane \underline{x} = \underline{X} \exp (j \omega t) = \frac{\underline{V}}{j\omega} \exp (j\omega t) s’obtient à partir de l’expression du débit :
\displaystyle{ \underline{X} = \frac{\underline{V}}{j \nu \omega_s} = \frac{\underline{Q}}{j \nu \omega_s S} = \frac{1}{j\nu \omega_s S} \frac{j\nu}{( j\nu)^2 +\frac{j\nu}{Q_{ts}} + 1} \cdot \omega_s C_{as} \underline{P}_g }
Soit :
\displaystyle{ \underline{X} = \underline{H}_X \cdot \frac{C_{as} \underline{P}_g}{S} }
avec \displaystyle{ \underline{H}_X = \frac{1}{( j\nu)^2 +\frac{j\nu}{Q_{ts}} + 1} }
dont le module est \displaystyle{ |\underline{H}_X| = \frac{1}{\sqrt{\nu^4 +\nu^2\left(-2+\frac{1}{Q_{ts}^2}\right) + 1} } }
Comme pour la puissance, il n’y aura donc pas de résonance pour un bon haut-parleur de facteur de qualité total égal ou très proche de 1/\sqrt{2}. Dans ce cas, le maximum de déplacement est à \nu=0 :

Valeurs maximales
Tension et puissance électrique
Le déplacement efficace du haut parleur est fonction de la tension imposée par l’amplificateur (présente dans l’expression de la pression d’excitation \underline{P}_g). La tension maximale admissible correspond donc à la tension pour laquelle le haut-parleur atteint son élongation linéaire maximale x_\text{max}.
Mais à quelle fréquence faire ce calcul ?
- D’un côté, le déplacement est maximal aux basses fréquences
- De l’autre, nous avons vu que la puissance s’effondre en attaquant le pic d’impédance du haut parleur.
On peut alors estimer la tension maximale nécessaire en faisant le calcul à la moitié du pic de l’impédance motionnelle : on sélectionne \omega_p tel que |\underline{Z_\text{mot}}|(\omega_p)=\frac{|\underline{Z}|_\text{mot,max}}{2}.

L’expression de l’impédance motionnelle peut se mettre sous la forme :
\displaystyle{ |Z_\text{mot,p}|^2=\left( \frac{R_\text{mot}}{2} \right)^2 = \frac{\omega_p^2 (Bl)^4}{(m + 2m_\text{R})^2\omega_p^4 + (\alpha^2 - 2 (m+2m_\text{R}) k) \omega_p^2 + k^2} }
La résolution de l’équation du second degré en \omega_p^2 conduit dans notre exemple à : f_p = 108 \,\text{Hz}.
Le déplacement de la membrane à prendre en compte pour ce calcul est donc :
\displaystyle{ |\underline{X}| = |\underline{H}_X(\omega_p)| \cdot \frac{C_{as} P_g} {S} }
Injectons l’expression de la pression d’excitation et imposons |\underline{X}|=x_\text{max}:
\displaystyle{ x_\text{max} = |\underline{H}_X(\omega_p)| \cdot \frac{C_{as} (Bl)\cdot U_\text{max}}{S^2\cdot R_e} = |\underline{H}_X(\omega_p)| \cdot \frac{(Bl)\cdot U_\text{max}}{k\cdot R_e} }Il vient :
\displaystyle{ U_\text{max} = \frac{1}{ |\underline{H}_X(\omega_p)| }\cdot \frac{k R_e x_\text{max}} {Bl} }
On trouve pour le woofer U_\text{max}=22\,\text{V}. La puissance maximale demandée à l’amplificateur est alors \mathcal{P}_{e,\text{max}} = \frac{U_\text{max}^2}{R_e}= 68\,\text W. Cette dernière est calculée non pas au pic d’impédance mais à sa valeur minimale \approx R_e. La fiche du haut-parleur indique 50 \,\text W_\text{RMS} et 100 \,\text W en crête, mais elle ne correspond qu’à des critères électriques et non acoustiques.
Niveau sonore maximal
On peut maintenant recalculer le niveau sonore avec la tension crête maximale que l’on vient d’obtenir :
\displaystyle{ L_\text{max}=10\, \log \frac{ U_\text{max}^2/2}{2\pi I_0} + 10\, \log \frac{\eta_0}{R_e} }Pour notre woofer, on obtient L_\text{max}=112\,\text{dB}. Comme nous le verrons dans le prochain article, et comme beaucoup d’autres résultats obtenus ici, cette valeur sera modifiée lorsqu’il sera placé dans un caisson.
Hautes fréquences
La puissance rayonnée a été calculée dans l’approximation des basses fréquences. Nous avons en effet utilisé le développement limité du facteur de rayonnement pour ka \ll 1, ce qui correspond à une fréquence limite pour notre exemple f \ll 830 \,\text{Hz}. De plus, la résistance de rayonnement aux hautes fréquences ne sera plus négligeable devant la résistance mécanique. Enfin, a découlé de l’approximation basse fréquence l’émission quasi-isotrope du haut parleur, et nous avons donc négligé sa directivité.
Tous les calculs précédents ne sont donc valables, comme on l’a déjà dit, que pour des fréquences inférieures à quelques centaines de Hertz. Mais le haut-parleur que nous étudions est annoncé pouvoir émettre de 93 Hz (sa fréquence de résonnance) à 5500 Hz.
Comparons le modèle que nous avons élaboré (en rouge) à la courbe de réponse mesurée du haut-parleur :

Le repère vertical bleu correspond à ka=1, le repère vertical rouge correspond à la fréquence maximale d’utilisation indiquée par le fabricant.
La droite jaune modélisant la coupure a une pente de 24 décibels par octave.
Si le modèle explicité dans cet article est très efficace pour déterminer les propriétés d’un haut-parleur aux basses fréquences, il s’avère insuffisant pour caractériser sa fréquence de coupure haute et les “accidents” parfois prononcés apparaissant sur la courbe de réponse. Le SP-165PA présente par exemple une chute brutale du niveau sonore autour de 1 kHz, puis des oscillations qui apparaissent au delà de 3 kHz.
Que peut-on prévoir du rayonnement du haut-paleur au delà de l’approximation des basses fréquences ? Ce sera l’objet d’un prochain article d’apporter des éléments de réponse.
Conclusion
Nous avons présenté dans cet article un modèle du haut-parleur électrodynamique encastré dans un baffle infini, permettant de comprendre les phénomènes à l’oeuvre derrière la courbe de réponse et de calculer précisément cette courbe à basse fréquence. Le domaine des basses fréquences est particulièrement utile pour prévoir la fréquence de coupure basse du haut-parleur, la puissance électrique requise, et le niveau sonore maximal attendu.
Dans le prochain article, nous verrons comment sont modifiées ces grandeurs lorsqu’on encastre le haut-parleur dans un caisson pour fabriquer une enceinte acoustique.
Sources
José-Philippe Pérez – Mécanique (DUNOD)
Francis BROUCHIER – Haut-parleurs et enceintes acoustiques : Théorie et pratique
Jean Fourcade – Utilitaires Scilab pour le calcul et l’optimisation d’enceintes bass-reflex

