Catégorie : Physique du son

Cet article fait suite à l’étude du haut-parleur électroacoustique. Nous verrons ici ce qu’il advient de ses propriétés et de son rayonnement lorsqu’il est intégré dans un caisson pour réaliser une enceinte.

• Résonance d’un haut-parleur monté dans un caisson
  • Variations de pression dans le caisson
  • Équation mécanique
  • Fréquence de résonance
• Rayonnement acoustique
  • Fonction de transfert
  • Phénomène de baffle (baffle-step)
  • Puissance rayonnée dans les deux modèles
  • Transition baffle step
  • Niveau sonore de l’enceinte close
• Diffraction par les bords
  • Position du problème
  • Cas d’un baffle circulaire
  • Observation hors-axe
  • Baffle rectangulaire
• Conclusion

Résonance d’un haut-parleur monté dans un caisson

Variations de pression dans le caisson

Nous avons vu que l’émission en opposition de phase de la face arrière de la membrane crée des interférences destructives néfastes, en particulier dans le domaine des basses fréquences. L’intégration du haut-parleur dans un caisson a pour objectif d’éviter ce court-circuit acoustique : le rayonnement arrière est en effet supprimé.

Soit $V_0$ le volume du caisson, enfermant de l’air à la pression atmosphérique $P_0$. Le volume d’air contenu dans le caisson étanche varie en fonction du déplacement de la membrane du haut-parleur de surface $S$ : lorsque l’élongation de la membrane est $x$, le volume d’air est $V=V_0 + \Delta V$ avec $\Delta V = S \cdot x$. L’air subit ainsi des successions de compressions et de dilatations au cours des vibrations de la membrane.

Si on suppose, comme d’habitude, que ces transformations sont adiabatiques, il résulte de la loi de Laplace :

$\displaystyle{ \frac{ \text d}{\text d V} \left( P\cdot V^\gamma \right) = 0 \iff \frac{ \text{d}P}{\text{d}V} = - \frac{\gamma P}{V} }$

Ainsi, si le volume $\Delta V$ balayé par la membrane reste petit devant le volume total du caisson $V_0$, la surpression résultante peut s’écrire :

$\displaystyle{ p = - \frac{\gamma P_0}{V_0} \Delta V = - \frac{\gamma P_0}{V_0} S x }$

Équation mécanique

Prenons pour guide l’application de la deuxième loi de Newton au haut-parleur vue précédemment, nous avions obtenu comme équation mécanique du haut-parleur :

$(m + 2m_\text{R}) \cdot \ddot{x} + (\alpha + 2R_\text{R}) \cdot \dot{x} + k \cdot x = Bl \cdot i$

Deux modifications doivent être réalisées dans la configuration de l’enceinte close :

• D’une part, le rayonnement arrière ayant été supprimé, le facteur 2 devant la résistance de rayonnement $R_\text{R}$ disparaît.
• D’autre part, la surpression $p$ de l’air enfermé dans le caisson ajoute une force $F$ dont l’expression est, d’après le résultat du paragraphe précédent : $F = p\cdot S = - \frac{\gamma P_0 S^2}{V_0} x$
  Cette expression est celle d’une force de rappel $F = - k_\text{a} \, x$, avec $k_\text{a} = \frac{\gamma P_0 S^2}{V_0}$ la raideur du volume d’air contenu dans le caisson.

Dans l’hypothèse où la surface de la membrane est petite en comparaison de la surface du panneau avant du caisson, la masse d’air déplacée à l’arrière de la membrane est sensiblement égale à celle déplacée à l’avant. La masse totale de l’équipage mobile restera donc $m+2m_R$

L’équation mécanique du haut-parleur monté dans un caisson est donc :

$\displaystyle{ \boxed{ (m + 2m_\text{R}) \cdot \ddot{x} + (\alpha + R_\text{R}) \cdot \dot{x} + \left( k + k_\text{a} \right) \cdot x = Bl \cdot i }}$

Le comportement du haut-parleur monté en enceinte close se déduit donc de celui du haut-parleur monté sur un baffle plan infini par les substitutions :

• $2R_\text R \rightarrow R_\text R$
• $k \rightarrow k_\text{b} = k + k_\text a$ avec $k_\text a = \frac{\gamma P_0 S^2}{V_0}$

Nous utiliserons l’indice $b$ (pour “box”) pour toutes les grandeurs relatives au haut-parleur monté dans un caisson.

Fréquence de résonance

En suivant la démarche que nous avions emprunté pour le haut parleur monté sur un baffle plan, on aboutit au schéma électrique équivalent du haut parleur monté dans un caisson :

La résistance et l’inductance motionnelles sont inchangées, mais la capacité motionnelle subit une modification :

$\displaystyle{\left\{ \begin{array}{ll} L_{\text{m,b}} = \frac{m +2m_\text{R}}{(Bl)^2}\\ R_{\text{m,b}} = \frac{(Bl)^2}{\alpha} \\ C_{\text{m,b}} = \frac{(Bl)^2}{k_\text b} \end{array}\right.}$

Il s’ensuit que la résonance du circuit motionnel R,L,C en parallèle se produira à la pulsation :

$\displaystyle{\left( \frac{\text{d}\underline{Z}_\text{mot}}{\text{d}\omega}\right)_{\omega=\omega_b} = 0 \iff \omega_b = \frac{1}{\sqrt{L_{\text{m,b}} \cdot C_{\text{m,b}}}} = \sqrt{\frac{k_b}{m + 2m_\text{R}}}}$

Le numérateur de l’expression est plus grand que dans le cas d’un montage sur baffle plan, et le dénominateur est le même : la fréquence de résonance du haut-parleur est donc augmentée lors de son installation dans un caisson.

Le haut-parleur monté dans un caisson aura donc une fréquence de coupure dans les basses plus élevée.

La perte d’émission dans les graves sera d’autant plus marquée que la raideur $k_\text a$ de l’air contenu dans le caisson sera importante, celle ci augmentant lorsque le volume $V_0$ du caisson diminue.La fréquence de coupure du haut-parleur sera multipliée par $\sqrt{2}$ lorsque $k_\text a = k$. Ce seuil donne l’ordre de grandeur du volume minimal du caisson à utiliser.

Il est d’usage d’introduire ici le volume d’air équivalent à la suspension $V_\text{as}$, généralement publié dans les données constructeur des haut-parleurs. La raideur $k$ du haut-parleur serait obtenue avec un volume d’air

$\boxed{ \displaystyle{ V_\text{as} = \frac{\gamma P_0 S^2}{k} }}$

Pour monter un haut-parleur en enceinte close sans trop augmenter la fréquence de coupure, il faudra donc un volume de caisson au moins quelques fois supérieur à $V_\text{as}$.

Exemple

Illustrons ces propos par un exemple numérique. Rappelons les données constructeur du haut-parleur Monacor SP-165PA que nous avions pris en exemple dans l’article précédent :

• Surface efficace de la membrane $S = 137\times10^{-4}\,\text{m}^2$
• Masse de l’équipage mobile (bobine + membrane) $m = 8,2\times10^{-3} \,\text{kg}$)
• Raideur de la suspension élastique $k = 4,0\times 10^{3} \,\text{N}\,\text{m}^{-1}$)
• Résistance mécanique de la suspension $\alpha= 1,2 \,\text{kg}\,\text{s}^{-1}$
• Résistance de la bobine $R_e = 6.9\,\Omega$
• Inductance de la bobine $L_e= 0,50 \times10^{-3} \,\text{H}$
• Facteur de force $Bl = 7,1 \,\text{T}\,\text{m}$

On a pour ce haut-parleur $\displaystyle{ V_\text{as} = 6,6 \,\text{L} }$. Si on choisit de le monter dans un caisson de volume $V_0=40\,\text{L} \approx 6 V_\text{as}$, on aura : $k_\text a = \frac{\gamma P_0 S^2}{V_0} = 6,7 \times 10^2 \,\text{N}\,\text{m}^{-1}$

La raideur totale sera : $k_\text b = k + k_\text a = 4,7 \times 10^3 \,\text{N}\,\text{m}^{-1}$

Et la pulsation de résonance : $\omega_\text b = \sqrt{\frac{k_b}{m + m_\text{R}}} = 654 \, \text{rad} \, \text{s}^{-1} = 1,08 \, \omega_0$

La fréquence de coupure aura ainsi augmenté de 8%, passant de 96 à 104 Hz.

Rayonnement acoustique

Fonction de transfert

Le schéma acoustique équivalent au haut-parleur monté dans un caisson est :

• Pression excitatrice $\underline{p}_g=\underline{P}_g \exp (j\omega t)$ avec $\underline{P}_g = \frac{(Bl)\cdot\underline{U}}{S\cdot R_e}$, exprimée en Pascals.
• Débit $\underline{q} = \underline{Q} \exp (j\omega t)$, en $\text{m}^3/\text{s}$
• Résistances acoustiques, en $\text{Pa}\cdot\text{s}/\text{m}^3$:
  • $R_{ae}=\frac{(Bl)^2}{S^2 R_e}$ (pertes électriques dans la bobine)
  • $R_{ab}=\frac{\alpha}{S^2}$ (pertes par frottements)
• La compliance acoustique en $\text{m}^3/\text{Pa}$ : $C_{ab}=\frac{S^2}{k_b}$.
• La masse acoustique en $\text{kg}/\text{m}^4$ : $M_{ab}=\frac{m + m_\text{R}}{S^2}$
• Résistance acoustique de rayonnement avant $R_{ar}=\frac{R_\text{R}}{S^2}$

Posons :

• $\delta = \frac{\omega_b}{\omega_s} = 1,08$;
• $Q_{eb} =\frac{1}{\omega_b C_{ab}R_{ae}}$ le facteur de qualité électrique ;
• $Q_{mb} =\frac{1}{\omega_b C_{ab}R_{ab}}$ le facteur de qualité mécanique ;
• $Q_{tb}$  le facteur de qualité total tel que $\frac{1}{Q_{tb}} = \frac{1}{Q_{eb}} + \frac{1}{Q_{mb}}$ .

Reprenons l’exemple du Monacor déjà étudié, monté dans un caisson de 40 L :

Montage sur baffle plan	Montage dans caisson de 40 L
$\omega_s = 606 \, \text{rad}\,\text{s}^{-1}$	$\omega_b = \delta \omega_s = 654 \, \text{rad}\,\text{s}^{-1}$
$Q_\text{es} = 1,1$	$Q_{eb}=1,0$
$Q_\text{ms} = 5,0$	$Q_\text{mb} = 4,6$
$Q_\text{ts} = 0,91$	$Q_\text{tb} = 0,83$

Les facteurs de qualité diminuent en intégrant le haut-parleur dans un caisson, et ce d’autant plus que le volume du caisson est petit.

L’expression du débit, obtenue en suivant la démarche exposée dans l’article précédent, est alors :

$\displaystyle{ \underline{Q}_b = \frac{j\delta \nu}{( j \delta \nu)^2 +\frac{j \delta \nu}{Q_{tb}} + 1} \cdot \omega_b C_{ab} \underline{P}_g = \frac{j\delta \nu}{( j \delta \nu)^2 +\frac{j \delta \nu}{Q_{tb}} + 1} \cdot \frac{ \omega_s C_{as}}{\delta} \underline{P}_g }$

où $\nu = \frac{\omega}{\omega_s}$ est la pulsation réduite définie par rapport à la pulsation de résonance du haut-parleur monté en baffle plan et où le deuxième terme a été réécrit en fonction des valeurs du haut-parleur monté en baffle plan.

Phénomène de baffle (baffle step)

Lorsque nous avons étudié le monopôle acoustique, nous avons signalé qu’il modélisait de manière très satisfaisante le rayonnement d’une enceinte close aux très basses fréquences. En effet, la longueur d’onde étant supérieure aux dimensions $L$ du baffle ($f < c / L$), celui-ci est invisible pour les ondes sonores émises. Le rayonnement est alors isotrope dans tout l’espace.

Puis nous avons étudié le modèle du piston encastré sur un baffle infini, qui modélise bien le rayonnement d’une enceinte aux fréquences supérieures ($f > c / L$) : la longueur d’onde étant plus petite que le baffle du caisson, les ondes sonores le voient comme un baffle de grande dimension. Le rayonnement se fait alors principalement dans le demi-espace avant. Tant que la longueur d’onde est supérieure au rayon $a$ du haut-parleur, ce rayonnement est lui aussi très peu directif.

Dans la fonction de transfert obtenue au paragraphe précédent, il faudra donc utiliser le modèle du monopôle pour les basses fréquences et celui du piston bafflé pour les fréquences supérieures. La transition entre ces deux modèles est appelée phénomène de baffle, ou baffle step en anglais.

Puissances rayonnées dans les deux modèles

La puissance rayonnée s’obtient à partir de la fonction de transfert de la même manière que nous l’avons obtenue pour le rayonnement du haut-parleur monté sur un baffle infini. La différence entre le rayonnement monopolaire (basse fréquence) et celui du piston bafflé (hautes fréquences) tient à la résistance de rayonnement $R_R$, qui est doublée pour le piston bafflé. On obtient ainsi pour le piston bafflé :

$\displaystyle{ { \mathcal{P}_{ar,b,\text{HF}} = \frac{\rho_0}{4\pi c} \left( \frac{\omega_s^2 C_{as} \underline{P}_g}{\delta^2} \right) ^2 \left|\underline{H}_{P,b}\right|^2} \hspace{1cm} \text{avec} \hspace{1cm}\underline{H}_{P,b} = \frac{\delta^2\nu^2}{( j\delta\nu)^2 +\frac{j\delta\nu}{Q_{tb}} + 1} }$

Dans le cas du monopôle, on obtient deux fois moins :

$\displaystyle{ { \mathcal{P}_{ar,b,\text{BF}} = \frac{\rho_0}{8\pi c} \left( \frac{\omega_s^2 C_{as} \underline{P}_g}{\delta^2} \right) ^2 \left|\underline{H}_{P,b}\right|^2}} = \frac{ \mathcal{P}_{ar,b,\text{HF}}}{2}$

Dans les basses fréquences, la valeur maximale de la puissance rayonnée est ainsi divisée par $2\delta^4$ par rapport au même haut-parleur monté en baffle plan. Afin d’optimiser la fréquence de coupure dans les basses et le niveau sonore, on aura donc tout intérêt à placer le haut-parleur dans un caisson de volume suffisamment grand pour que $\delta$ soit proche de 1.

Le rendement $\eta_b$ du haut-parleur monté dans une enceinte close est lui calculé dans les hautes fréquences, lorsque $\left|\underline{H}_{P,b}\right| \approx 1$ : on a donc $\eta_b = \frac{\eta_0}{\delta^4}$. Pour notre exemple, on obtient $0,6\%$.

La sensibilité $L_{1,b}$ de l’enceinte est quant à elle réduite de $10\cdot \log{\delta^4}$, soit une chute de $1,3\,\text{dB}$ pour l’enceinte considérée : on obtient $L_1 = 90,2\,\text{dB}$.

Transition baffle step

Aux hautes fréquences, les ondes sonores sont émises dans le demi-espace avant du caisson. A une distance $r$ de l’enceinte, la puissance émise se dilue sur une demi-sphère de surface $2\pi r^2$ et l’intensité sonore est :

$\displaystyle{ I_\text{HF} = \frac{ \mathcal{P}_{ar,b,\text{HF}} }{2\pi r^2}}$

Aux basses fréquences, les ondes sonores sont émises dans tout l’espace, la surface sur laquelle se dilue l’énergie est donc $4\pi r^2$. On a alors :

$\displaystyle{ I_\text{BF} = \frac{ \mathcal{P}_{ar,b,\text{BF}} }{4\pi r^2} = \frac{I_\text{HF}}{4}}$

La transition liée au phénomène de baffle s’accompagne donc d’une diminution de $6\text{dB}$ dans les graves.

Sur quelles fréquences s’étale le phénomène de baffle ?

La diffraction est quantifiée par l’angle $\theta$ d’étalement de l’onde. Pour l’obstacle de dimension $L$ qu’est le caisson de l’enceinte, on a :

$\theta = \frac{\lambda}{L}$

Une onde émise par le haut-parleur le long du baffle sera significativement diffractée vers l’arrière dès lors que $\theta \approx \frac{\pi}{4}$. Cela correspond à $\lambda_1 \approx 0,7L$. Le rayonnement deviendra isotrope dans l’espace lorsque $\theta \approx 2\pi$, soit $\lambda_2 \approx 6 L$. La fréquence de transition est celle pour laquelle l’atténuation est moitié de sa valeur maximale, soit :

$f_\text{step} = \sqrt{f_1 f_2} = \sqrt{\frac{c^2}{\lambda_1\lambda_2} } \approx \frac{1}{2} \frac{c}{L}$
$f_1 \approx 3 \, f_\text{step}, f_2 \approx \frac{f_\text{step}}{3}$

Ou encore

$\lambda_\text{step} = \frac{c}{f_\text{step}} \approx 2L$
$\lambda_1 \approx \frac{\lambda_\text{step}}{3}, \lambda_2 \approx 3 \, \lambda_\text{step}$

On peut construire un bon modèle mathématique de la transition à l’aide d’une approximation bien connue de la fonction step de Heavyside :

$H(f) \approx 6 \times \left( \left( 1 + \exp{ \left( -2 k \ln{\frac{f}{f_\text{step}}} \right) } \right)^{-1} -1 \right)$

avec $k=2$ permettant l’étalement du phénomène sur l’intervalle $\left[ \frac{f_\text{step}}{3} ; 3 \, f_\text{step} \right]$ :

Niveau sonore de l’enceinte close

Nous pouvons donc maintenant calculer l’intensité sonore aux hautes fréquences avec l’expression obtenue plus haut, en déduire le niveau sonore et prendre en compte la transition vers un rayonnement monopolaire aux basses fréquences en lui ajoutant la transition baffle step.

Pour notre enceinte de 40L, choisissons une profondeur du caisson de 25 cm et un baffle circulaire de 22,5 cm de rayon, le haut-parleur étant monté au centre de celui-ci. Je ne vous conseille pas une telle géométrie, mais elle permet de n’avoir qu’une unique dimension $L=0,45 \,\text{m}$ à considérer. On obtient, avec un phénomène de baffle à 380 Hz s’étalant de 127 Hz à 1.14 kHz :

Notons tout de même que, dans un cas réel d’écoute dans une pièce, une fraction non négligeable des ondes sonores graves émises vers l’arrière de l’enceinte sera réfléchie par les murs, augmentant de fait le niveau perçu des basses. Le phénomène de baffle provoquera donc plutôt une diminution de 2 à 4 dB que de 6dB.

Notons aussi que, lorsque le caisson est rectangulaire, la transition sera adoucie du fait de fréquences de transition différentes pour les différentes tailles de l’obstacle vues par l’onde :

Par exemple, pour un même volume de caisson de 40L et une même profondeur de 25cm, un baffle rectangulaire de dimension $30 \times 50 \,\text{cm}$ aura une transition de phénomène de baffle qui s’étendra de $\lambda_1 \approx 0,7 \,L_{min}=21\,\text{cm}$ à $\lambda_{max} \approx 6 \,L_{max}=3,0 \,\text{m}$, soit :

$f_{min}=114\,\text{Hz} \,\, ; \,\, f_{max}=1,63\,\text{kHz}, \,\,f_\text{step}=\sqrt{f_{min}f_{max}}=430\,\text{Hz}$

Diffraction par les bords

Position du problème

On s’intéresse dans cette section au côté “hautes-fréquences” du phénomène de baffle : les ondes sonores sont supposées contraintes à se propager dans un demi-espace délimité par le baffle.

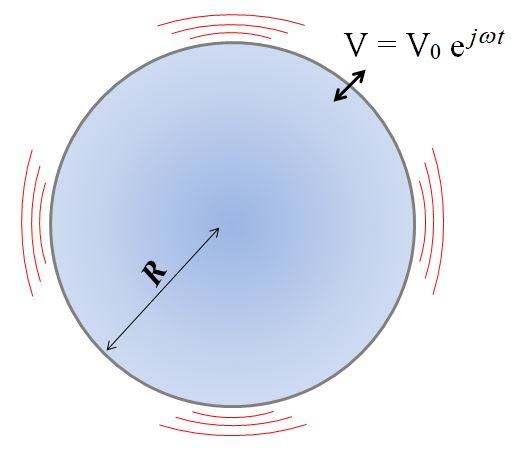
Considérons une onde sphérique. Le principe d’Huygens-Fresnel stipule que chaque point du milieu perturbé par l’onde devient lui-même une source élémentaire secondaire, la combinaison des perturbations générées par ces sources secondaires constituant le nouveau front d’onde :

Lorsque l’onde se propageant le long du baffle atteint sa périphérie, elle rencontre une discontinuité puisque le volume disponible pour sa propagation change : il passe d’une demi-sphère à une sphère. La pression chute d’un facteur 2 et les sources secondaires ne forment alors plus un ensemble cohérent avec leur prédécesseurs, il faut les considérer comme une nouvelle source. On parle de diffraction par le bord du baffle.

Du fait de leur déphasage, provenant du délai induit par la propagation jusqu’au bord du baffle, l’onde directe et l’onde diffractée interfèrent au point d’observation : la pression acoustique présentera des pics lorsque les ondes sont en phase et des creux lorsqu’elles sont en opposition de phase.

Cas d’un baffle circulaire

Dans un souci de simplification visant à se concentrer sur les effets physiques, nous nous restreindrons dans un premier temps au cas défavorable d’un baffle circulaire observé dans l’axe.

Nous nous intéressons ici au haute-fréquences : changeons donc notre haut-parleur d’étude pour un tweeter Dayton DC28FT de rayon $a=14 \,\text{mm}$, de fréquence de résonance $f_s = 834 \,\text{Hz}$ et de facteur de qualité total $Q_\text{ts} = 0,50$. Ce haut-parleur est monté dans une enceinte close, au centre d’un baffle circulaire de rayon $R= 22,5 \,\text{cm}$. Il n’y a pas de modification de la fréquence de résonance pour le tweeter : il est monté en usine dans un caisson étanche (le caisson servirait, dans un cas réel d’enceinte deux-voies, à supprimer le court-circuit acoustique du HP de graves).

Sa courbe de réponse théorique est alors, en tenant compte du phénomène de baffle :

La distance parcourue par l’onde en atteignant le bord du baffle est égale aux rayon $R$ du baffle. Le bord du baffle se comporte donc comme une deuxième source émettant à la même fréquence que le haut parleur mais avec un retard $\tau = R/c$, durée nécessaire pour atteindre le bord du baffle en partant de son centre.

L’onde directe se propageant dans un demi-espace a pour expression au point M :

$\displaystyle{ p_0 = \frac{j \omega \rho Q_0}{2\pi} \cdot \frac{\exp{j \left( \omega t - k r_0\right) }} {r_0} }$

L’onde diffractée émise par une source secondaire infinitésimale de longueur $\text{d}\mathcal{l} = R\cdot \text{d}\varphi$ s’écrit quant à elle:

$\displaystyle{ \text{d}p_1 = D(0) \cdot \frac{j \omega \rho Q_0}{4\pi} \cdot \frac{ \exp{ \left[ j \left( \omega t - k \left(r_1+R\right) \right)\right]} } {r_1 + R} \cdot \frac{\text{d}\varphi}{2\pi} }$

où $D(0)$ est le facteur de directivité du haut-parleur le long du baffle.

En champ lointain, on a $r_1 \approx r_0$ et la différence d’amplitude due à la distance parcourue supplémentaire $R$ est négligeable. Il vient :

$\displaystyle{ \text{d}p_1 = D(0) \cdot \frac{1}{2} \cdot p_0 \cdot \exp{\left( -j k R \right)}\frac{\text{d}\varphi}{2\pi} }$

L’intégration le long du cercle est triviale, finalement :

$\displaystyle{ p_1 = D(0) \cdot \frac{1}{2} \cdot p_0 \cdot \exp{\left( -j k R \right)} }$

La pression résultante au point d’observation est donc :

$\displaystyle{ p = p_0 + p_1 = p_0 \left( 1 + D(0) \cdot \frac{1}{2} \exp{ \left(- jkR \right) } \right) }$

Les ondes directes et diffractées interfèrent au point d’observation via le terme entre parenthèses ; la pression acoustique efficace est :

$\displaystyle{ p_\text{eff} = \frac{ \left| p \right| }{\sqrt{2}} = p_{0,\text{eff}} \left( 1 + D(0) \cdot \frac{1}{2} \cos{ \left(kR\right) }\right) }$

Les interférences seront constructives lorsque les ondes directe et diffractée sont en phase au point d’observation, i.e. lorsque $k R = m \cdot2\pi$ avec $m$ entier positif, soit $\lambda = R/m$ ou encore $f = m c /R$. Les ondes seront en opposition de phase, générant des interférences destructives, lorsque $k R = \left( m + \frac{1}{2} \right) \cdot2\pi$, soit $\lambda = R/\left( m + \frac{1}{2} \right)$ ou encore $f = \left( m + \frac{1}{2}\right) c /R$.

Le haut-parleur devenant très directif aux hautes fréquences ($ka >= 4$, le phénomène s’estompe :

Les variations de niveau sonore sont donc de l’ordre de 10 dB au maximum (la pression variant d’un facteur 3 entre 0,5 et 1,5, l’intensité sonore varie d’un facteur 9 et $10 \times \log{9} = 9,5$.

On peut maintenant calculer l’intensité sonore $I=\frac{p_\text{eff}^2}{\rho c}$ et le niveau sonore résultant :

Le premier creux, correspondant à $\lambda / 2 = R$, est masqué partiellement par le phénomène de baffle (la longueur d’onde est grande, le rayonnement de l’enceinte se fait donc quasiment sur une sphère et il y a peu de diffraction). La première bosse en fin de transition baffle-step correspond à $\lambda = R$ puis le creux suivant à $\lambda = \frac{2}{3}R$, etc.

Observons un agrandissement de la zone d’intérêt, en échelle linéaire de fréquence :

Les pics sont espacés d’environ 1500 Hz, la longueur d’onde correspondante est $\lambda = \frac{c}{f} = 22,8\,\text{cm}$ : on peut ainsi mesurer le rayon du baffle.

Notons ici que l’amplitude des variations sera amoindrie avec des arrêtes arrondies.

Observation hors-axe

On se place maintenant hors-axe, dans un direction définie par l’angle $\eta$ par rapport à l’axe de symétrie du baffle :

Un peu de géométrie permet de voir que la différence de marche supplémentaire de l’onde diffractée par rapport à l’onde directe est $\delta = R \sin{\eta}\cos{\varphi}$, le déphasage correspondant est $\phi_0 = k\delta$.

L’onde directe a donc pour expression :

$\displaystyle{ p_0 = D\left(\frac{\pi}{2}-\eta\right) \cdot \frac{j \omega \rho Q_0}{2\pi} \cdot \frac{\exp{j \left( \omega t - k r_0\right) }} {r_0} }$

Et on aura au point d’observation, pour source secondaire infinitésimale $\text{d}p_1$ :

$\displaystyle{ \text{d}p_1 = D(0) \cdot \frac{1}{2} \cdot p_0 \cdot \exp{\left( -j k (R - \delta) \right)}\frac{\text{d}\varphi}{2\pi} }$

L’onde diffractée par le bord du baffle est ainsi :

$\displaystyle{ p_1 = D(0) \cdot \frac{1}{2} \cdot p_0 \cdot \exp{\left( -j k R\right)} \cdot \int_0^{2\pi} \exp{\left( j k R\sin{\eta}\cos{\varphi}) \right)} \frac{\text{d}\varphi}{2\pi} }$

L’intégrale dans le dernier terme est : $J_0\left(k R \sin(\eta)\right)$, fonction de Bessel d’ordre 0 :

$\displaystyle{ p_1 = D(0) \cdot \frac{1}{2} \cdot p_0 \cdot \exp{\left( -j k R\right)} \cdot J_0\left(k R \sin(\eta)\right) }$

En sommant l’onde directe $p_0$ (affectée du facteur de directivité $D(\frac{\pi}{2}-\eta)$ et l’onde diffractée $p_1$, puis en calculant l’intensité sonore correspondante et en en déduisant le niveau sonore de la même manière que précédemment, on obtient les courbes suivantes :

On constate sans surprise que la diffraction par les bords est moindre hors-axe : en effet, les différentes sources secondaires sur le pourtour du baffle ne sont plus toutes en phase. Ce calcul montre que, lorsqu’on cherche à corriger les pics et les creux dans l’axe par un filtrage numérique, on génère de fait des pics et des creux hors-axe.

Baffle rectangulaire

Penchons nous dorénavant sur le cas plus concret du baffle rectangulaire, observé dans l’axe. Sa géométrie est résumée sur la figure suivante :

Nous avons gardé les dimensions du caisson utilisé dans le calcul du phénomène de baffle : $L_1=50\,\text{cm}$, $L_2=30\,\text{cm}$. Le tweeter est positionné aux coordonnées $x_t = y_t = 20\,\text{cm}$.

L’expression de l’onde directe est identique à celle obtenue dans le cas du baffle circulaire, et une source infinitésimale située à la coordonnée $\varphi$ engendrera au point d’observation, avec les mêmes simplifications que précédemment :

$\displaystyle{ \text{d}p_1 = D(0) \cdot \frac{1}{2} \cdot p_0 \cdot \exp{\left( -j k b(\varphi) \right)}\frac{\text{d}\varphi}{2\pi} }$

L’intégration se fait numériquement, par morceaux pour chacune des arêtes du baffle. Par exemple, pour l’arrête supérieure, on aura :

$\displaystyle{ p_{1,\text{top}} = D(0) \cdot \frac{1}{2} \cdot p_0 \cdot \int_{\arctan{\frac{L_1-y_t}{L_2-x_t}}}^{\frac{\pi}{2}+\arctan{\frac{x_t}{L_1-y_t}}} {\exp{\left( -j k \frac{L_1-y_t}{\sin{\varphi}} \right)}\frac{\text{d}\varphi}{2\pi} } }$

Le terme d’interférences a l’allure donnée ci-dessous.

On en déduit comme plus haut le niveau sonore du haut-parleur monté dans le caisson :

Comme on pouvait s’y attendre, les effets de la diffraction par les bords du baffle sont nettement moins prononcés qu’avec un baffle circulaire (les sources secondaires ne sont en effet jamais toutes en phase avec l’onde directe). Ici, comme pour le baffle circulaire, la mesure des écarts en fréquence des différents pics permet de déduire la distance entre le haut-parleur et les bords du baffle. Par exemple, les deux pics les plus visibles sur le graphe sont espacés de 3400 Hz, ce qui correspond à une longueur d’onde de 10 cm, distance séparant le haut-parleur du haut du baffle.

L’étude de la directivité est, elle aussi, réalisée par intégration numérique en ajoutant comme dans le cas du baffle circulaire la différence de marche supplémentaire $\delta = b(\varphi)\cdot\sin{\eta}\cdot\cos{\varphi}$ :

Conclusion

Nous avons vu dans cet article les conséquences sur le rayonnement acoustique du scellement d’un haut-parleur dans un caisson : augmentation de la fréquence de résonance, phénomène de baffle et diffraction par les bords du baffle.

Un moyen possible de contrer l’augmentation de la fréquence de résonance et donc de la coupure grave du haut-parleur est d’intégrer un évent dans le caisson pour réaliser une enceinte bass-reflex. Le prochain article y sera consacré.

Sources

Francis BROUCHIER – Haut-parleurs et enceintes acoustiques : Théorie et pratique

Jean Fourcade – Utilitaires Scilab pour le calcul et l’optimisation d’enceintes bass-reflex

Loudspeaker Cabinet Diffraction (Tore Skogberg)

Diffraction from baffle edges

Après avoir traité les bases de l’acoustique et le rayonnement acoustique, cet article aborde la problématique de la production d’ondes sonores avec un haut-parleur électroacoustique. Nous nous appuierons sur ce que nous y avons appris et nous utiliserons le principe de l’induction électromagnétique ainsi qu’un peu de mécanique pour comprendre le fonctionnement d’un haut-parleur électrodynamique. Le modèle que nous dresserons nous permettra d’isoler les grandeurs physiques importantes et de discuter de l’ordre de grandeur de leurs valeurs.

• Données techniques d’un haut-parleur
  • Description
  • Jeu de paramètres
• Equation mécanique
  • Force de Lorentz
  • Force de Laplace exercée sur un conducteur
  • Cas particulier de la bobine d’un haut-parleur
  • Principe fondamental de la dynamique
• Equation électrique
  • Force électromotrice induite
  • Loi des mailles
• Impédance
  • Solution en régime sinusoïdal forcé
  • Circuit électrique équivalent
• Rayonnement acoustique
  • Circuit acoustique équivalent
  • Débit acoustique
  • Puissance rayonnée
  • Rendement
  • Niveau sonore, sensibilité
  • Déplacement de la membrane
• Valeurs maximales
  • Tension et puissance électrique
  • Niveau sonore
• Hautes fréquences
• Conclusion

Données techniques d’un haut-parleur

Description

Jeu de paramètres

• Surface efficace de la membrane $S = 137\times10^{-4}\,\text{m}^2$
• Masse de l’équipage mobile (bobine + membrane) $m = 8,2\times10^{-3} \,\text{kg}$)
• Raideur de la suspension élastique $k = 4,0\times 10^{3} \,\text{N}\,\text{m}^{-1}$) (on trouve fréquemment son inverse, la compliance $C = 1/k$ de la suspension en $\text{m}\,\text{N}^{-1}$)
• Résistance mécanique de la suspension $\alpha= 1,2 \,\text{kg}\,\text{s}^{-1}$ (coefficient de la vitesse dans l’expression de la force de frottement fluide)
• Résistance de la bobine $R_e = 6.9\,\Omega$ (l’indice $e$ se réfère aux grandeurs électriques)
• Inductance de la bobine $L_e= 0,50 \times10^{-3} \,\text{H}$
• Facteur de force $Bl = 7,1 \,\text{T}\,\text{m}$ (produit du champ magnétique par la longueur de la bobine)

À quoi nous rajoutons la valeur limite du déplacement de la membrane pour laquelle la réponse est linéaire : $x_\text{max} = 3,75 \times10^{-3} \,\text{m}$

Equation mécanique

Force de Lorentz

En sommant ces deux forces, on obtient la force de Lorentz qui s’exerce sur une particule chargée plongée dans un champ électromagnétique :

$\vec{F}=q \cdot (\,\vec{E} + \vec{v} \land \vec{B})\,$

Force de Laplace exercée sur un conducteur

Soit un circuit électrique filiforme, parcouru par un courant $I$, en mouvement dans un champ électromagnétique $(\, \vec{E},\,\vec{B} )\,$ à la vitesse $\vec{V}$.

Toutes les particules chargées du conducteur (ions métalliques et électrons libres) sont soumises à la force de Lorentz.

Pour les ions métalliques, de charge positive, $e$ correspondant à la charge élémentaire :

$\vec{F}_{ion}=e \cdot (\,\vec{E} + \vec{V} \land \vec{B})\,$

Pour les électrons libres, de charge opposée en mouvement à la vitesse $\vec{u}$ dans le circuit :

$\vec{F}_{elec}=-e \cdot (\,\vec{E} + (\,\vec{V} + \vec{u})\,\land \vec{B})\,$

Il y a autant d’ions métalliques que d’électrons libres. Toutes les contributions s’annulent sauf celle due à la vitesse propre des électrons dans le circuit. La force exercée globalement sur le circuit, appelée force de Laplace, est donc la somme de toutes les forces $\vec{f}=-e \vec{u}\land \vec{B}$ exercées sur chacun des électrons libres.

Cas particulier de la bobine d’un haut-parleur

Pour simplifier la suite, plaçons-nous d’ores et déjà dans la géométrie qui nous intéresse pour l’étude du haut parleur. Le conducteur est une bobine de fil de longueur totale $l$ plongée dans un champ magnétique radial d’intensité $B$ :

D’après la règle de la main droite, pour un courant circulant dans le sens horaire (et donc des électrons circulant dans le sens trigonométrique) toutes les forces à sommer sont donc colinéaire à l’axe central du dispositif, dirigées suivant les $x$ croissants. C’est la convention choisie sur les haut-parleurs : la borne teintée de rouge ou indiquée “+” correspond au sens de branchement pour lequel un courant positif met l’équipage mobile en mouvement vers l’extérieur. Il nous reste à sommer les contributions $\vec{f}=-e\cdot u\cdot B \cdot \vec{e}_x$ pour chacun des électrons libres ($\vec{e}_x$ est le vecteur unitaire portant l’axe $x$).

Combien y-a-t-il d’électrons libres dans cette bobine ? Le courant étant le débit de charges, il y a $n=I/e$ électrons qui traversent une section du circuit en une seconde. Les derniers à la traverser sont ceux qui étaient situés à une distance $\delta = u \times 1\,\text{s}$ une seconde auparavant. Si $l$ est la longueur totale du fil, il y en a donc $\frac{l}{\delta}$ fois plus : il y a en tout $N = n \cdot \frac{l}{\delta}=\frac{I \cdot l}{u\cdot e}$ électrons libres. La force de Laplace exercée sur la bobine est finalement :

$\vec{F}_L=N \cdot \vec{f}=\frac{I \cdot l}{u\cdot e} \cdot (\,-e)\,\cdot u\cdot B \cdot \vec{e}_x=I \cdot Bl \cdot \vec{e}_x$

Si la bobine est parcourure par un courant d’intensité constante $i$, la force de Laplace exercée sur elle sera donc constante elle aussi. Mais si, maintenant, on impose un courant variable $i$ dans la bobine, on voit que la force de Laplace sera elle aussi variable. Elle poussera la bobine tantôt à droite (lorsque le courant est positif) et tantôt à gauche (lorqu’il est négatif). L’effet sera donc de faire vibrer la bobine autour de sa position d’équilibre.

L’énergie mécanique vibratoire pourra alors être transmise en partie à l’air, comme nous l’avons détaillé dans l’article précédent.

Notons enfin que la force de Laplace est proportionnelle au facteur de force $Bl$ affiché par les constructeurs.

Principe fondamental de la dynamique

Appliquons le principe fondamental de la dynamique au système {bobine + membrane} de masse $m$ dans le référentiel de l’aimant : $m \cdot \vec{a} = \Sigma\, \vec{F}_\text{ext}$.

Les forces exercées suivant l’axe $x$ sont :

• la force de rappel $-k\cdot x$ due à la fixation élastique, qui ramène le système vers sa position d’équilibre ;
• une force dissipative de frottements fluides proportionnelle à la vitesse du système $-\alpha \cdot v_x = -\alpha \cdot \dot{x}$ ;
• la force de Laplace $Bl \cdot i$ exercée sur la bobine ;
• les forces de pression $-p_\text{avant} S$ et $p_\text{arrière} S$ dues à la pression de l’air sur les faces de la membrane. Ces forces caractérisent le rayonnement acoustique du haut-parleur.

Nous avons vu que les forces de pression pouvaient s’écrire : $Z_\text{R} \cdot \dot{x}$, avec $Z_\text{R} = R_\text{R} + j \omega m_\text{R}$ l’impédance de rayonnement. Les expressions de la résistance de rayonnement $R_\text{R}$ et de la masse de rayonnement $m_\text{R}$ sont, pour un piston encastré dans un plan infini, dans l’approximation des basses fréquences :

$\displaystyle{ R_\text{R} \approx \rho c S \sigma = \frac{\rho_0 S^2 }{2\pi c}\omega^2 \hspace{1cm}\text{et} \hspace{1cm} m_\text{R} \approx \frac{8\rho}{3}\left(\frac{S}{\pi}\right)^{3/2} }$

Pour le haut-parleur Monacor pris en exemple, on obtient :

$\displaystyle{ R_\text{R} \approx 1,0\times10^{-7}\omega^2 \;\text{kg}\,\text{s}^{-1}\hspace{1cm}\text{et} \hspace{1cm} m_\text{R} \approx 0,9 \,\text{g} }$

La résistance de rayonnement est donc négligeable devant la résistance mécanique jusqu’à $\omega \approx 10^3 \,\text{rad}\,\text{s}^{-1}$. L’expression utilisée n’est de toute manière valable qu’aux basses fréquences. La masse de rayonnement quant à elle implique une faible correction de l’ordre de quelques pourcents.

Contrairement au modèle du piston solide, la membrane du haut-parleur est en contact avec l’air des deux côtés du baffle : masse de rayonnement et résistance de rayonnement sont à prendre en compte pour le rayonnement avant et pour le rayonnement arrière.

On obtient donc l’équation différentielle relative à la position de la bobine (équation mécanique du haut-parleur) :

$(m + 2m_\text{R}) \cdot \ddot{x} = -k \cdot x - (\alpha + 2R_\text{R})\cdot \dot{x} + Bl \cdot i$

Equation électrique

Force électromotrice induite

Lorsqu’un circuit est mobile dans un champ magnétique, la force magnétique exercée sur les électrons libres va les mettre en mouvement. Un courant induit apparaît donc spontanément dans le circuit. On appelle force électromotrice $u_\text{ind}$ la différence de potentiel expliquant l’apparition de ce courant électrique. Nous établirons dans ce paragraphe l’expression de la f.e.m. induite dans la bobine d’un haut parleur en mouvement dans le champ magnétique de l’aimant.

Dans le référentiel de l’aimant, il règne dans l’entrefer un champ magnétique $\vec{B}$ radial. Lorsque la bobine est en mouvement à la vitesse $\vec{V}$, les électrons libres subissent une force de Lorentz $\vec{F}=-e \cdot \vec{V} \land \vec{B}$. D’après la règle de la main droite, cette force aura tendance à mettre les électrons en mouvement dans le sens trigonométrique, et donc à générer un courant positif dans la bobine. En appelant $\vec{u}$ le vecteur unitaire dirigé en chaque point de la bobine dans le sens d’une intensité positive : $\vec{F}= e \cdot V \cdot B \cdot \vec{u}$.

Plaçons nous maintenant dans le référentiel de la bobine. On vient de voir que des électrons initialement immobiles se mettront en mouvement dans le sens horaire. Ils sont donc soumis à l’effet d’un champ électrique $\vec{E}'$ qui s’écrit, par définition :

$\displaystyle{ \vec{E}' = \frac{\vec{F}}{q} = \frac{e \cdot V \cdot B \cdot \vec{u}}{-e}= V \cdot B \cdot \vec{u} }$

La force électromotrice induite est égale à la circulation du champ électrique entre les deux extrémités de la bobine ;

$u_\text{ind}= \int_0^l \vec{E}' \cdot \text d \vec{l} =- V \cdot Bl$

Loi des mailles

La loi des mailles donne :

$u(t)\, + u_\text{ind}(t)\, = u_R + u_L \, \iff \, R \cdot i + L \cdot \frac{\text{d}i}{\text{dt}} = u(t)\, - Bl \cdot \dot{x}$

Cette équation est appelée équation électrique du haut-parleur. Elle est donc, sans surprise, l’équation d’un circuit R,L en régime forcé. Mais la tension forçant le circuit contient deux termes : la tension imposée et la f.e.m. due à la vitesse de la bobine.

Impédance

Solution en régime sinusoïdal forcé

Nous avons vu que la résistance de rayonnement est faible devant le coefficient de frottement mécanique : $R_\text{R} \ll \alpha$. Nous négligerons donc le terme contenant $R_\text{R}$ dans cette section qui ne traite que du comportement électrique du haut-parleur.

Un haut-parleur est donc régi par deux équations :

$\left\{ \begin{array}{ll} (m + 2m_\text{R})\cdot \ddot{x} + \alpha \cdot \dot{x} + k \cdot x = Bl \cdot i \\ R \cdot i + L \cdot \frac{\text{d}i}{\text{dt}} = u(\,t)\, - Bl\cdot \dot{x} \end{array}\right.$

Ces deux équations sont couplées, puisque l’équation mécanique contient la variable électrique $i$ et que l’équation électrique contient la variable mécanique $x$. Les coefficients de couplage sont respectivement $Bl$ et $- Bl$ : ils sont opposés.

Recherchons des solutions particulières de ces équations en imposant un régime sinusoïdal. Un son plus complexe sera décrit par un ensemble de fréquences, et donc par une somme de sinusoïdes, comme expliqué ici. Imposons donc dans l’équation mécanique une intensité sinusoïdale $\underline{i}=\underline{I} \cdot \exp{(\,j \omega t)\,}$. Nous utilisons ici la notation complexe.

Injectons maintenant dans l’équation une solution sinusoïdale pour $x$, c’est à dire une solution s’écrivant sous la forme $\underline{x}=\underline{X} \cdot \exp{(\,j \omega t)\,}$. On obtient :

$\left[(m + 2m_\text{R}) (j \omega)^2 + j \omega \alpha + k \right] \cdot \underline{X} = Bl \cdot \underline{I}$

En opérant de la même manière pour l’équation électrique :

$\underline{U} - Bl \cdot \underline{\dot{X}}= \left( R + j \omega L \right) \underline{I}$

Eliminons $\underline{X}$ de la deuxième équation en utilisant la première :

$\displaystyle{\underline{\dot{X}} = \frac{ j \omega \cdot Bl}{(m + 2m_\text{R}) (j\omega)^2 +j \omega \alpha + k} \cdot \underline{I}}$

$\displaystyle{\underline{U} = \left( R + j \omega L + \frac{j \cdot \omega \cdot (Bl)^2}{(m + 2m_\text{R}) (j\omega) ^2 +j \omega \alpha + k}\right)\underline{I}}$

Où l’impédance électrique du haut-parleur $\underline{Z} = \underline{U} / \underline{I}$ apparaît :

$\displaystyle{\underline{Z} = R + j \omega L + \frac{j \omega \cdot (Bl)^2}{(m + 2m_\text{R}) (j\omega)^2 -j \omega \alpha + k} }$

Le terme $R + j \omega L$ est l’impédance électrique classique d’une bobine, le deuxième terme est dû au mouvement de la bobine dans le champ magnétique de l’aimant et est appelé impédance motionnelle :

$\displaystyle{\underline{Z}_{\text{mot}} = \frac{j \omega \cdot l^2 \cdot B^2}{(m + 2m_\text{R}) \omega ^2 -j \omega \alpha - k} }$

Circuit électrique équivalent

Remarquons maintenant que l’impédance motionnelle peut s’écrire :

$\displaystyle{\underline{Z}_{\text{mot}} = \frac{1}{\frac{j \omega (m + 2m_\text{R})}{(Bl)^2} + \frac{\alpha}{(Bl)^2} +\frac{k}{j \omega (Bl)^2}} }$

Soit :

$\displaystyle{\frac{1}{\underline{Z}_{\text{mot}}} = \frac{1}{j \omega L_\text{mot}}+ \frac{1}{R_\text{mot}} + \frac{1}{\frac{1}{j\omega C_\text{mot}} } }$

avec

$\displaystyle{\left\{ \begin{array}{ll} L_{\text{mot}} = \frac{m + 2m_\text{R}}{(Bl)^2}\\ R_{\text{mot}} = \frac{(Bl)^2}{\alpha} \\ C_{\text{mot}} = \frac{(Bl)^2}{k} \end{array}\right.}$

On reconnait ainsi l’association en parallèle d’un condensateur de capacité $C_{\text{mot}}$, d’un résistor de résistance $R_{\text{mot}}$ et d’une bobine d’inductance $L_{\text{mot}}$.

Pour le haut-parleur utilisé en exemple, on obtient :

• $C_{\text{mot}} = 198 \,\text{µF}$
• $R_\text{mot} = 42,0 \,\Omega$
• $L_\text{mot}= 12,6 \,\text{mH}$

Prenons un instant pour comprendre l’origine physique de ces trois effets. La masse en mouvement permet le stockage d’énergie (du fait de l’inertie) comme une bobine stocke de l’énergie magnétique lorsque des charges la traversent. Les forces de frottement dissipent de l’énergie comme le fait une résistance par effet Joule. Enfin, la raideur du ressort permet, par la force de rappel, le stockage d’énergie élastique, comme un condensateur stocke de l’énergie électrique par accumulation de charges.

Le schéma électrique équivalent d’un haut-parleur est finalement :

La résonance du circuit motionnel $R_{\text{mot}}, \, L_{\text{mot}} , \, C_{\text{mot}}$ en parallèle se produit à la pulsation

$\displaystyle{\left( \frac{\text{d}\underline{Z}_\text{mot}}{\text{d}\omega}\right)_{\omega=\omega_0} = 0 \iff \omega_0 = \frac{1}{\sqrt{L_{\text{mot}} \cdot C_{\text{mot}}}} = \sqrt{\frac{k}{m + 2m_\text{R}}}}$.

Dans notre exemple, $\omega_0 = 606\,\text{rad}\,\text{s}^{-1}$ soit $f_0 = 96\,\text{Hz}$. Le pic du module d’impédance est $|\underline{Z}|_\text{max}=R_e+R_\text{mot}=49\,\Omega$.

Deux faits importants à noter ici :

• Le pic d’impédance à la fréquence de résonance $f_0 = \frac{\omega_0}{2\pi}$ implique que le haut-parleur ne peut pas générer de son de fréquence inférieure. Cette fréquence constitue donc la limite basse de la bande passante. En effet, bien que commercialisé en affichant sa puissance, un amplificateur est bien un amplificateur de tension. Or la puissance est $\mathcal{P} = \frac{U^2}{|\underline{Z}|}$: elle s’effondre en s’approchant du pic d’impédance.
• Aux basses fréquences, l’impédance électrique du haut parleur est quasiment résistive : $\underline{Z}_{e} = R_e + j\omega L_e \approx R_e$. Mais lorsque la pulsation s’approche de la valeur $\omega = R_e/L_e$ (dans notre exemple proche de $14 000 \,\text{rad}\,\text{s}^{-1}$), les effets inductifs commencent à apparaître et l’impédance remonte.
• Entre ces deux valeurs, le module de l’impédance passe par un minimum $Z$, qui est l’impédance affichée par le constructeur.

Seules les performances acoustiques d’un haut-parleur sont, in fine, d’intérêt. L’étude électrique a cependant d’intéressant que la mesure de la courbe d’impédance, plus simple à réaliser avec précision qu’une mesure acoustique, permet de déterminer certaines caractéristiques acoustiques du haut-parleur (résistance motionnelle, pulsation de résonance).

Rayonnement acoustique

Circuit acoustique équivalent

Repartons maintenant de l’équation mécanique et de l’équation électrique et éliminons le courant de l’équation mécanique. On obtient sans difficulté :

$\displaystyle{\frac{Bl\cdot\underline{U}}{R_e+j\omega L_e} = \left[ j\omega (m+2m_\text{R}) + (\alpha + 2R_\text{R}) + \frac{k}{j\omega} + \frac{(Bl)^2}{R_e + j\omega L_e} \right] \cdot \underline{\dot{X}} }$

Il s’agit d’une égalité entre termes de la dimension d’une force, soit une énergie par unité de longueur. En divisant par la surface du haut-parleur $S$, on obtient donc une égalité entre pressions (le Pascal est une énergie par unité de volume):

$\displaystyle{ \frac{(Bl)\cdot\underline{U}}{S(R_e+j\omega L_e)} = \left[ \frac{ j\omega (m+2m_\text{R})}{S^2} + \frac{\alpha + 2R_\text{R}}{S^2} + \frac{k}{j\omega S^2} + \frac{(Bl)^2}{S^2(R_e + j\omega L_e)} \right] \cdot \underline{Q}}$

où $\underline{q} = S \cdot \dot{\underline{x}} = \underline{Q} \exp{(j \omega t)}$ est le débit du haut-parleur.

Aux basses-fréquences ($\omega \ll R_e/L_e$), le terme de gauche est indépendant de la fréquence:

$\displaystyle{ \frac{(Bl)\cdot\underline{U}}{S\cdot R_e} = \left[ j\omega \frac{m + 2m_\text{R}}{S^2} + \frac{\alpha + 2R_\text{R}}{S^2} + \frac{1}{j\omega} \frac{k}{S^2} + \frac{(Bl)^2}{S^2\cdot R_e} \right] \cdot \underline{Q}}$

On obtient alors une équation “électrique” décrivant une association en série de quatre résistances, un condensateur et une bobine :

$\displaystyle{ \underline{P}_g = \left(R_{ae} + R_{as} + \frac{1}{j\omega \, C_{as}} + j\omega M_{as}+R_{ar,1}+R_{ar,2} \right) \cdot \underline{Q}}$

Avec :

• L’équivalent de la tension est la pression excitatrice $\underline{p}_g=\underline{P}_g \exp (j\omega t)$ avec $\underline{P}_g = \frac{(Bl)\cdot\underline{U}}{S\cdot R_e}$, exprimée en Pascals.
• Le courant correspondant est le débit $\underline{q} = \underline{Q} \exp (j\omega t)$, en $\text{m}^3/\text{s}$
• Les résistances acoustiques sont, en $\text{Pa}\cdot\text{s}/\text{m}^3$:
  • $R_{ae}=\frac{(Bl)^2}{S^2 R_e}$ (pertes électriques dans la bobine)
  • $R_{as}=\frac{\alpha}{S^2}$ (pertes par frottements)
• La compliance acoustique (équivalent d’une capacité) est, en $\text{m}^3/\text{Pa}$ : $C_{as}=\frac{S^2}{k}$. La compliance, très utilisée en acoustique, est l’inverse de la raideur.
• La masse acoustique (équivalent d’une inductance) est, en $\text{kg}/\text{m}^4$ : $M_{as}=\frac{m + 2m_\text{R}}{S^2}$
• Les résistances acoustiques de rayonnement avant $R_{ar,1}=\frac{R_\text{R}}{S^2}$ et arrière $R_{ar,2}= R_{ar,1}$

L’indice $s$ suivant l’indice “acoustique” $a$ correspond au haut-parleur (speaker) seul. Nous le changerons pour un $b$ (box) lorsqu’il sera encastré dans un caisson et que les grandeurs correspondantes en seront modifiées.

On peut maintenant résoudre le problème physique par analogie avec un circuit électrique. Le circuit équivalent est le suivant :

Débit acoustique

Nous pouvons ici aussi, compte tenu du faible rendement des haut-parleurs,négliger les résistances de rayonnement dans le calcul du débit du haut-parleur. La fonction de transfert du haut-parleur s’écrit alors :

$\displaystyle{  \underline{Q} = \frac{1}{R_{ae} + R_{as} + \frac{1}{j\omega \, C_{as}} + j\omega M_{as}}\cdot \underline{P}_g }$

$\displaystyle{ \iff \underline{Q} = \frac{1}{( j\omega)^2 C_{as} M_{as} + j \omega C_{as}R_{ae} + j \omega C_{as}R_{as} + 1} \cdot j \omega C_{as} \underline{P}_g }$

C’est la fonction de transfert d’un oscillateur amorti par les termes résistifs, qui se comporte donc comme un filtre passe-bande. Sa pulsation de résonance est : $\omega_s^2 = 1/(C_{as}M_{as}) = k/(m + 2m_\text{R}) = \omega_0^2$. La résonance du débit a donc lieu a la fréquence correspondant au pic d’impédance électrique.

Posons :

• $\nu = \omega / \omega_s$ la pulsation réduite ;
• $Q_{es} =\frac{1}{\omega_s C_{as}R_{ae}}$ le facteur de qualité électrique (pour le Monacor étudié $Q_{es} = 1,11$) ;
• $Q_{ms} =\frac{1}{\omega_s C_{as}R_{as}}$ le facteur de qualité mécanique (pour le Monacor : $Q_{ms}= 5,0$).

L’expression du débit devient :

$\displaystyle{ \underline{Q} = \frac{j\nu}{( j\nu)^2 + j\nu \left(\frac{1}{Q_{es}}+ \frac{1}{Q_{ms}}\right) + 1} \cdot \omega_s C_{as} \underline{P}_g }$

Posons enfin $Q_{ts}$  le facteur de qualité total tel que $\frac{1}{Q_{ts}} = \frac{1}{Q_{es}} + \frac{1}{Q_{ms}}$ (pour l’exemple, on a $Q_{ts} = 0,91$ ):

$\displaystyle{\boxed{ \underline{Q} = \frac{j\nu}{( j\nu)^2 +\frac{j\nu}{Q_{ts}} + 1} \cdot \omega_s C_{as} \underline{P}_g }}$

Puissance rayonnée

On sait que :

$\displaystyle{ \mathcal{P}_{ar} = R_\text{R} V_\text{eff}^2 = \frac{R_\text{R}}{S^2} Q_\text{eff}^2 = \frac{R_\text{R}}{2 S^2} |Q|^2}$

Par ailleurs $R_\text{R} = \rho_0 c S \sigma$. Il vient :

$\displaystyle{ \mathcal{P}_{ar} = \frac{\rho_0 c \sigma}{2 S} |Q|^2}$

Nous sommes ici en approximation basse fréquence vis à vis des caractéristiques du haut-parleur ($\omega \ll \frac{R_e}{L_e}$). Les basses fréquences vis à vis des caractéristiques acoustiques sont définies par $ka \ll 1 \iff \omega \ll \frac{c}{a}$ ($a$ étant le rayon du haut-parleur).

Pour notre exemple, on a $a = \sqrt{S/\pi} = 0,066 \, \text{m}$ : $\omega \ll \frac{c}{a} \approx 5 000 \, \text{rad}\cdot \text s ^{-1} \approx 800 \, \text{Hz}$

Ces deux approximations sont donc du même ordre de grandeur. Dans leur respect ($f < 300 \, \text{Hz}$), le facteur de rayonnement du haut parleur bafflé est bien, comme on l’a déjà utilisé plus haut, $\sigma \approx \frac{a^2 k^2}{2} = \frac{S}{2\pi c^2}\omega^2$. Il vient :

$\displaystyle{ \mathcal{P}_{ar} = \frac{\rho_0 }{4\pi c}\omega^2|Q|^2 }$

La courbe de réponse du haut-parleur en basse fréquence est alors, en injectant l’expression de l’amplitude du débit :

$\displaystyle{ \boxed{ \mathcal{P}_{ar} = \frac{\rho_0 \left( \omega_s^2 C_{as} \underline{P}_g \right) ^2}{4\pi c} \left|\underline{H}_P\right|^2} \hspace{1cm} \text{avec} \hspace{1cm} \boxed{\underline{H}_P = \frac{\nu^2}{( j\nu)^2 +\frac{j\nu}{Q_{ts}} + 1} }}$

Sous la forme $a+jb$, la fonction de transfert s’écrit :

$\displaystyle{ \underline{H}_P = \frac{ \displaystyle{\frac{\nu^3}{Q_{ts}}}+j \nu^2 (1-\nu^2)} {\nu^4 + \nu^2 \left(-2 + \displaystyle{\frac{1}{Q_{ts}^2}} \right) + 1} }$

Le carré de son module est :

$\displaystyle{ |\underline{H}_P|^2 = \frac{\nu^4} {\nu^4 + \nu^2 \left(-2 + \displaystyle{\frac{1}{Q_{ts}^2}} \right) + 1} }$

À basse fréquence $\nu \rightarrow 0$, un développement limité donne : $|\underline{H}_P|^2 \approx \nu^4$. Le comportement asymptotique du niveau sonore est donc une droite de pente 12 dB/octave (la puissance est en effet multipliée par $2^4=16$  lorsque la fréquence double).

L’allure du carré du module de la fonction de transfert est la suivante :

On voit sur l’expression précédente qu’il n’y aura de résonance (courbes rouge et violette ci-dessus) que si $-2 + \frac{1}{Q_{ts}^2} < 0 \iff Q_{ts} > 1/\sqrt{2}$. Un bon haut-parleur assurera une transition douce vers les graves et ne présentera donc pas de pic de puissance prononcé : il aura un facteur de qualité maximal $Q_{ts} \leq \frac{1}{\sqrt{2}}$.

La coupure à $3\,\text{dB}$ se produit pour $|\underline{H}_P|^2 = \frac{1}{2}$, soit pour :

$\nu_3^2 = \left( \frac{1}{2Q_{ts}^2}-1\right) + \sqrt{1+\left( \frac{1}{2Q_{ts}^2}-1\right)^2}$

En valeurs numériques :

Pour qu’il assure aussi une puissance maximale jusqu’à la coupure (au contraire des courbes bleue et orange qui s’effondrent tôt), un bon haut parleur aura donc un facteur de qualité total proche de $Q_{ts} \approx 1/\sqrt{2} \approx 0,7$ (courbe verte).

Notre haut-parleur d’étude, de $Q_{ts} \approx 0,9$, est proche de la courbe rouge. Du point de vue de la coupure à -3 dB dans les basses, il est plutôt bon. De celui d’une transition douce vers le basses, ce n’est pas un excellent choix.

Rendement

Le rendement du haut-parleur est :

$\displaystyle{ \eta = \frac{\mathcal{P}_{ar}}{\mathcal{P}_e} }$

où $\mathcal{P}_e = \frac{U_\text{eff}^2}{|\underline{Z}|}$ est la puissance électrique consommée par le haut-parleur. Ces grandeurs dépendant de la fréquence, le rendement sera évalué au minimum du module d’impédance, pour lequel $|\underline{Z}| \approx R_e$ et $|\underline{H}_P| = 1$. Alors :

$\displaystyle{ \eta_0 = \frac{\rho_0}{4\pi c} \frac{ \left(\omega_s^2 C_{as} \underline{P}_g \right) ^2}{U_\text{eff}^2/R_e} }$

En développant l’expression de la pression d’excitation, il vient :

$\displaystyle{ \eta_0 = \frac{\rho_0}{4\pi c} \frac{ \left(\omega_s^2 C_{as} \frac{(Bl)\sqrt{2}U_\text{eff}}{S\cdot R_e} \right) ^2}{U_\text{eff}^2/R_e} = \frac{\rho_0}{2\pi R_e c} \left( \frac{\omega_s^2 C_{as}(Bl)}{S} \right) ^2 }$

Expression qui devient, en fonction uniquement de données constructeur :

$\displaystyle{ \boxed{ \eta_0 = \frac{\rho_0}{2\pi R_e c} \left( \frac{S(Bl)}{m + 2m_\text{R}} \right) ^2 }}$

L’application numérique pour le woofer étudié donne : $\eta_0 = 0,8\%$.

Le rendement d’un haut-parleur est généralement inférieur à 1%, ce qui justifie d’une autre manière d’avoir négligé dans les calculs précédents la résistance de rayonnement.

Niveau sonore, sensibilité

En champ lointain, le rayonnement de la membrane est isotrope. L’intensité sonore à une distance $r$ s’obtient donc en divisant la puissance acoustique par la surface de la demi-sphère sur laquelle se dilue l’énergie :

$I = \displaystyle{ \frac{\mathcal{P}_{ar}}{2\pi r^2} = \frac{\rho_0}{8\pi^2 c}\left(\frac{\omega_s^2 C_{as} \underline{P}_g}{r} \right)^2 \left| \underline{H}_P \right|^2 }$

Le niveau sonore est, par définition :

$L=10\, \log \frac{I}{I_0}$

La sensibilité $L_1$ d’un haut-parleur est le niveau sonore obtenu à une distance de $r_0 = 1 \,\text{m}$ du haut-parleur lorsqu’il est alimenté par une tension efficace $U_\text{eff}= 2,83V$ (qui correspond, pour une impédance de $8 \Omega$, à une puissance électrique moyenne $\mathcal{P}_e = U_\text{eff}^2/Z=1\,\text{W}$). La sensibilité est évaluée dans la plage de fréquence où le haut-parleur est le plus efficace ($|\underline{H}_P| = 1$).

On peut écrire, avec cette définition :

$\displaystyle{ L_1=10\, \log \frac{\eta_0 U_\text{eff}^2 / (2\pi R_e)}{I_0}=10\, \log \frac{ U_\text{eff}^2}{2\pi I_0} + 10\, \log \frac{\eta_0}{R_e} = 121,1 + 10\, \log \frac{\eta_0}{R_e} }$

Cette relation donne, appliquée au woofer : $L_1 = 91,5\,\text{dB}$.

Déplacement de la membrane

L’excursion de la membrane $\underline{x} = \underline{X} \exp (j \omega t) = \frac{\underline{V}}{j\omega} \exp (j\omega t)$ s’obtient à partir de l’expression du débit :

$\displaystyle{ \underline{X} = \frac{\underline{V}}{j \nu \omega_s} = \frac{\underline{Q}}{j \nu \omega_s S} = \frac{1}{j\nu \omega_s S} \frac{j\nu}{( j\nu)^2 +\frac{j\nu}{Q_{ts}} + 1} \cdot \omega_s C_{as} \underline{P}_g }$

Soit :

$\displaystyle{ \underline{X} = \underline{H}_X \cdot \frac{C_{as} \underline{P}_g}{S} }$

avec $\displaystyle{ \underline{H}_X = \frac{1}{( j\nu)^2 +\frac{j\nu}{Q_{ts}} + 1} }$

dont le module est $\displaystyle{ |\underline{H}_X| = \frac{1}{\sqrt{\nu^4 +\nu^2\left(-2+\frac{1}{Q_{ts}^2}\right) + 1} } }$

Comme pour la puissance, il n’y aura donc pas de résonance pour un bon haut-parleur de facteur de qualité total égal ou très proche de $1/\sqrt{2}$. Dans ce cas, le maximum de déplacement est à $\nu=0$ :

Valeurs maximales

Tension et puissance électrique

Le déplacement efficace du haut parleur est fonction de la tension imposée par l’amplificateur (présente dans l’expression de la pression d’excitation $\underline{P}_g$). La tension maximale admissible correspond donc à la tension pour laquelle le haut-parleur atteint son élongation linéaire maximale $x_\text{max}$.

Mais à quelle fréquence faire ce calcul ?

• D’un côté, le déplacement est maximal aux basses fréquences
• De l’autre, nous avons vu que la puissance s’effondre en attaquant le pic d’impédance du haut parleur.

On peut alors estimer la tension maximale nécessaire en faisant le calcul à la moitié du pic de l’impédance motionnelle : on sélectionne $\omega_p$ tel que $|\underline{Z_\text{mot}}|(\omega_p)=\frac{|\underline{Z}|_\text{mot,max}}{2}$.

L’expression de l’impédance motionnelle peut se mettre sous la forme :

$\displaystyle{ |Z_\text{mot,p}|^2=\left( \frac{R_\text{mot}}{2} \right)^2 = \frac{\omega_p^2 (Bl)^4}{(m + 2m_\text{R})^2\omega_p^4 + (\alpha^2 - 2 (m+2m_\text{R}) k) \omega_p^2 + k^2} }$

La résolution de l’équation du second degré en $\omega_p^2$ conduit dans notre exemple à : $f_p = 108 \,\text{Hz}$.

Le déplacement de la membrane à prendre en compte pour ce calcul est donc :

$\displaystyle{ |\underline{X}| = |\underline{H}_X(\omega_p)| \cdot \frac{C_{as} P_g} {S} }$

Injectons l’expression de la pression d’excitation et imposons $|\underline{X}|=x_\text{max}$:

$\displaystyle{ x_\text{max} = |\underline{H}_X(\omega_p)| \cdot \frac{C_{as} (Bl)\cdot U_\text{max}}{S^2\cdot R_e} = |\underline{H}_X(\omega_p)| \cdot \frac{(Bl)\cdot U_\text{max}}{k\cdot R_e} }$

Il vient :

$\displaystyle{ U_\text{max} = \frac{1}{ |\underline{H}_X(\omega_p)| }\cdot \frac{k R_e x_\text{max}} {Bl} }$

On trouve pour le woofer $U_\text{max}=22\,\text{V}$. La puissance maximale demandée à l’amplificateur est alors $\mathcal{P}_{e,\text{max}} = \frac{U_\text{max}^2}{R_e}= 68\,\text W$. Cette dernière est calculée non pas au pic d’impédance mais à sa valeur minimale $\approx R_e$. La fiche du haut-parleur indique $50 \,\text W_\text{RMS}$ et $100 \,\text W$ en crête, mais elle ne correspond qu’à des critères électriques et non acoustiques.

Niveau sonore maximal

On peut maintenant recalculer le niveau sonore avec la tension crête maximale que l’on vient d’obtenir :

$\displaystyle{ L_\text{max}=10\, \log \frac{ U_\text{max}^2/2}{2\pi I_0} + 10\, \log \frac{\eta_0}{R_e} }$

Pour notre woofer, on obtient $L_\text{max}=112\,\text{dB}$. Comme nous le verrons dans le prochain article, et comme beaucoup d’autres résultats obtenus ici, cette valeur sera modifiée lorsqu’il sera placé dans un caisson.

Hautes fréquences

La puissance rayonnée a été calculée dans l’approximation des basses fréquences. Nous avons en effet utilisé le développement limité du facteur de rayonnement pour $ka \ll 1$, ce qui correspond à une fréquence limite pour notre exemple $f \ll 830 \,\text{Hz}$. De plus, la résistance de rayonnement aux hautes fréquences ne sera plus négligeable devant la résistance mécanique. Enfin, a découlé de l’approximation basse fréquence l’émission quasi-isotrope du haut parleur, et nous avons donc négligé sa directivité.

Tous les calculs précédents ne sont donc valables, comme on l’a déjà dit, que pour des fréquences inférieures à quelques centaines de Hertz. Mais le haut-parleur que nous étudions est annoncé pouvoir émettre de 93 Hz (sa fréquence de résonnance) à 5500 Hz.

Comparons le modèle que nous avons élaboré (en rouge) à la courbe de réponse mesurée du haut-parleur :

Si le modèle explicité dans cet article est très efficace pour déterminer les propriétés d’un haut-parleur aux basses fréquences, il s’avère insuffisant pour caractériser sa fréquence de coupure haute et les “accidents” parfois prononcés apparaissant sur la courbe de réponse. Le SP-165PA présente par exemple une chute brutale du niveau sonore autour de 1 kHz, puis des oscillations qui apparaissent au delà de 3 kHz.

Que peut-on prévoir du rayonnement du haut-paleur au delà de l’approximation des basses fréquences ? Ce sera l’objet d’un prochain article d’apporter des éléments de réponse.

Conclusion

Nous avons présenté dans cet article un modèle du haut-parleur électrodynamique encastré dans un baffle infini, permettant de comprendre les phénomènes à l’oeuvre derrière la courbe de réponse et de calculer précisément cette courbe à basse fréquence. Le domaine des basses fréquences est particulièrement utile pour prévoir la fréquence de coupure basse du haut-parleur, la puissance électrique requise, et le niveau sonore maximal attendu.

Dans le prochain article, nous verrons comment sont modifiées ces grandeurs lorsqu’on encastre le haut-parleur dans un caisson pour fabriquer une enceinte acoustique.

Sources

José-Philippe Pérez – Mécanique (DUNOD)

Modélisation électrique et acoustique du haut-parleur : impédance électrique et bande passante acoustique

Francis BROUCHIER – Haut-parleurs et enceintes acoustiques : Théorie et pratique

Jean Fourcade – Utilitaires Scilab pour le calcul et l’optimisation d’enceintes bass-reflex