Après avoir introduit les bases de l’acoustique, nous nous intéresserons dans cet article au rayonnement d’énergie acoustique. Nous verrons comment utiliser les formules d’acoustique déjà établies pour calculer l’intensité sonore générée par un solide en vibration. Nous nous concentrerons sur les trois cas dont nous aurons besoin pour comprendre, plus tard, le rayonnement acoustique d’un haut-parleur : la sphère pulsante, le dipôle acoustique, et le piston encastré.
Modèle de la sphère pulsante
Description
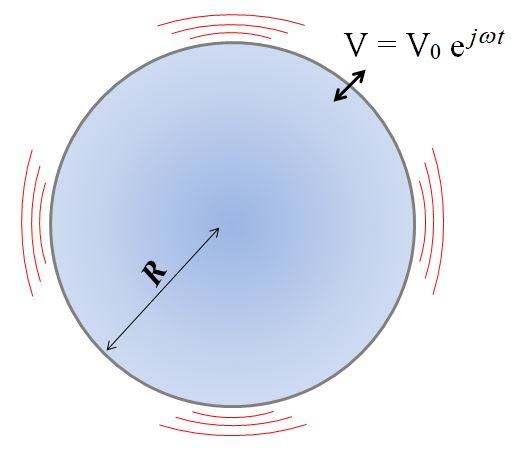
La source considérée ici est une sphère solide de rayon R dont la surface oscille à la vitesse uniforme \underline{V} = V_0 \exp{(j \omega t)}. L’amplitude des oscillations est supposée faible par rapport au rayon R. La pression de l’air est ainsi perturbée et une onde sonore sinusoïdale se propage.

La symétrie du problème indique que les grandeurs acoustiques ne dépendent que du temps et de la distance r entre l’origine et le point considéré. Les ondes sonores émises par la sphère pulsante sont donc sphériques.
Pression et vitesse acoustiques
Les formules correspondantes dans le cas des ondes sphériques sont :
\displaystyle{ \underline{p} = \frac{\underline{A}}{r} \exp{ \left[ j(\omega t - kr) \right] } }
\displaystyle{ \underline{u}_r = \left( 1 - \frac{j}{kr}\right) \frac{\underline{p}}{\rho_0 c} }
À l’interface entre la sphère et l’air, la vitesse de l’air est égale à celle de la surface de la sphère. La constante \underline{A} peut donc être déterminée. Injectons l’expression de la pression dans celle de la vitesse pour r = R, et égalisons avec l’expression de la vitesse de la surface de la sphère :
\displaystyle{ \underline{u}_r (R) = \left( 1 - \frac{j}{kR}\right) \frac{\underline{A}}{\rho_0 c R} \exp{ \left[ j(\omega t - kR)\right] } = V_0 \exp{(j\omega t)} }
On obtient :
\displaystyle{ \underline{A} = \rho_0 c R V_0 \frac{ \exp{(jkR)} }{1-\frac{j}{kR}} = j \omega \rho_0 R^2 V_0 \frac{ \exp{(jkR)} }{1 + jkR} }
Remarquons que cette “constante” dépend de la fréquence de vibration de la source !
La pression acoustique est donc :
\displaystyle{ \underline{p} = j \omega \rho_0 R^2 V_0 \frac{\exp{(jkR)} }{1 + jkR} \frac{\exp{ \left[ j(\omega t - kr) \right] }}{r} }
On définit maintenant le débit Q de la source comme le volume déplacé lors de ses vibrations par unité de temps : Q = Q_0 \exp{(j\omega t)} = 4 \pi R^2 V . L’expression de \underline{p} devient :
\displaystyle{ \underline{p} = \frac{ j \omega \rho_0 Q_0}{4\pi} \cdot \frac{\exp{(jkR)}}{1 + jkR} \cdot \frac{\exp{ \left[ j(\omega t - kr) \right] }}{r} }
Quant à celle de la vitesse acoustique \underline{u}:
\displaystyle{ \underline{u}_r = \left( 1 - \frac{j}{kr}\right) \frac{ j \omega Q_0}{4\pi c} \cdot \frac{\exp{(jkR)}}{1 + jkR} \cdot \frac{\exp{ \left[ j(\omega t - kr) \right] }}{r} = \left( 1 + jkr \right) \frac{ Q_0}{4\pi} \cdot \frac{\exp{(jkR)}}{1 + jkR} \cdot \frac{\exp{ \left[ j(\omega t - kr) \right] }}{r^2}}
Le monopôle acoustique
Il est difficile de concevoir un haut-parleur dont la membrane est une sphère, et on pourrait douter de l’importance du calcul précédent … Cependant, le modèle de la sphère pulsante nous sera d’une grande utilité pour les deux raisons suivantes :
- Lorsque les longueurs d’onde sont grandes par rapport aux dimensions de l’enceinte, il est vérifié expérimentalement que le rayonnement acoustique produit est très proche de celui d’une sphère pulsante. On peut le vérifier facilement en tournant autour d’une enceinte : les basses fréquences sonnent aussi clairement à l’arrière qu’à l’avant, ce qui n’est pas le cas des aigus.La sphère pulsante est donc un bon modèle pour les graves d’un enceinte, même si seule une partie de la surface de la sphère vibre. Pour les dimensions des radios TSF que nous utilisons, de l’ordre de 50 cm, on pourra décrire correctement par ce modèle des longueurs d’onde supérieures à 1,5m, ce qui correspond en gros à des fréquences inférieures à 200 Hz.
- Enfin, en vertu du principe d’Huygens-Fresnel, on pourra décrire plus bas une source vibrante complexe (la membrane d’un haut-parleur) en la considérant comme une somme de sources élémentaires sphériques.
Remarquons que, dans ces deux applications, les dimensions R de la source sont faibles (relativement pour la première, infinitésimale pour la deuxième). On peut donc simplifier les expressions en faisant tendre le rayon de la sphère vers zéro pour obtenir les expressions du monopôle acoustique :
\displaystyle{ \boxed{ \underline{p} = \frac{ j \omega \rho_0 Q_0}{4\pi} \cdot \frac{\exp{ \left[ j(\omega t - kr) \right] }}{r} }}\displaystyle{\underline{u}_r = \left( 1 + jkr \right) \frac{ Q_0}{4\pi} \cdot \frac{\exp{ \left[ j(\omega t - kr) \right] }}{r^2}}Intensité et niveau sonore
Nous avons déjà montré que, pour une onde sphérique : \displaystyle{ I = \frac{p_\text{eff}^2}{\rho_0 c}}
Ainsi, l’intensité sonore de l’onde produite par un monopôle acoustique est :
\displaystyle{\boxed{ I = \frac{\rho_0 }{2c} \left( \frac{ \omega Q_0}{4\pi r} \right)^2 } }
Comme nous l’avions déjà signalé en parlant de l’atténuation géométrique, l’intensité sonore décroît comme le carré de la distance à la source. L’énergie émise se dilue en effet sur une surface qui augmente comme le carré de la distance.
Le niveau sonore généré par le monopôle en découle :
L(r) = 10 \log{ \frac{I(r)}{I_0} } = 10 \log{ \left[ \frac{\rho_0 }{2 I_0 c} \left( \frac{ \omega Q_0}{4\pi r} \right)^2 \right]} = 10 \log{ \left( \frac{\rho_0 }{32 \pi^2 I_0 c}\right) + 20 \log \left( \frac{ \omega Q_0}{r} \right)}
où, après la dernière égalité, les seules grandeurs variables sont regroupées dans le dernier terme.
Enfin, la puissance acoustique \mathcal{P}_\text{s} émise par la source est calculable en sommant l’intensité sonore sur une sphére centrée sur la source de rayon r\prime quelconque :
\mathcal{P}_\text{ac} = 4\pi r\prime^2 I(r\prime) \iff \displaystyle{\boxed{ \mathcal{P}_\text{ac} = \frac{\rho_0 }{8\pi c} \left( \omega Q_0\right)^2 }}
Impédance de rayonnement
Expression
Retournons à la sphère pulsante de rayon R non infinitésimal. En vibrant, elle génère des variations de pression de l’air dans son voisinage. Ces variations de pression génèrent, à leur tour, une force sur la surface de la source. Il y a donc un phénomène de couplage entre la source et le milieu qu’elle perturbe.
Cette force s’écrit naturellement : \underline{f} = - \underline{p}(R) \cdot S
où S = 4 \pi R^2 est la surface de la sphère pulsante, et où le signe négatif provient du fait que la force exercée par l’air est dirigée vers les r décroissants.
On a montré que :
\displaystyle{ \underline{p}(R) = j \omega \rho_0 R^2 V_0 \frac{\exp{(jkR)} }{1 + jkR} \frac{\exp{ \left[ j(\omega t - kR) \right] }}{R} = \rho_0 R j \omega V_0 \exp{ (j\omega t)} \frac{1 }{1 + jkR}}On a vu que le modèle de la sphère pulsante n’était valide qu’aux basses fréquences, soit kR \ll 1. Un développement limité au premier ordre mène à \left( 1 + jkR \right)^{-1} \approx 1 - jkR :
\displaystyle{ \underline{p}(R) \approx \rho_0 R (1 - jkR) j \omega V_0 \exp{ (j\omega t)} = \rho_0 (1-jkR) j \omega \underline{V} = \left[ \frac{\rho R \omega^2}{c} + j \omega \rho_0 R \right] \underline{V} }La force exercée par l’air sur la structure vibrante est ainsi :
\underline{f} = \left[- \frac{\rho R S \omega^2}{c} - j \omega \rho_0 R S \right] \underline{V}
On définit l’impédance de rayonnement Z_{\text{ray}} comme le rapport de la force \underline{f}\prime = -\underline{f} exercée par la surface vibrante sur l’air sur la vitesse acoustique \underline{u}(R) = \underline{V}(R) générée :
\displaystyle{ Z_{\text{R}} = \frac{-\underline{f}}{\underline{u}} = \frac{\rho R S \omega^2}{c} + j \omega \rho_0 R S}
Cette grandeur traduit la résistance qu’a l’air à vibrer sous l’action de la force.
Masse et résistance de rayonnement
Remarquons enfin que j \omega V_0 \exp{ (j\omega t)} correspond à l’accélération \underline{a} d’un point de la surface vibrante, de sorte que la force peut s’écrire :
\displaystyle{ \underline{f} \approx -\rho_0 R S \underline{a} - \frac{\rho_0 R^2 \omega^2 S}{c} \underline{V} }
Le coefficient \rho_0 R S de l’accélération est homogène à une masse qu’on nommera masse de rayonnement m_\text{R}. Le deuxième terme, quant à lui, est une force de frottement fluide du type -R_\text{R} \underline{V}. R_\text{R} = \frac{\rho_0 R^2 \omega^2 S}{c} est appelée la résistance de rayonnement.
Ainsi, lorsqu’on cherchera l’équation du mouvement de l’équipage mobile d’un haut parleur, la deuxième loi de Newton s’écrira :
m \underline{a} = \Sigma \left(\text{autres forces}\right) + \underline{f}
\iff (m + m_\text{R}) \underline{a} = \Sigma \left(\text{autres forces}\right) - R_\text{R} \underline{V}
La masse de rayonnement s’interprète comme une masse d’air se mouvant de concert avec la source vibrante. La résistance de rayonnement quant à elle est le coefficient de frottement traduisant la conversion d’énergie mécanique en énergie acoustique : elle explique le rayonnement acoustique de la structure.
Avec ces notations, l’impédance de rayonnement s’écrit :
\displaystyle{ \boxed{ Z_{\text{R}} = R_\text{R} + j \omega \, m_\text{R} }}
où
\displaystyle{R_\text{R} = \frac{\rho_0 S^2\omega^2 }{4\pi c} } \hspace{2cm}m_\text{R}= \rho_0 \frac{S^{3/2}}{2\sqrt{\pi}}
Si la masse de rayonnement de la sphère pulsante a la bienveillance d’être constante, il n’en est pas de même pour la résistance de rayonnement qui varie comme le carré de la pulsation. On voit sur son expression que la conversion d’énergie mécanique de vibration de la source en énergie acoustique se fera très mal à basses fréquences. Voyons cela en détail.
Facteur de rayonnement
Le facteur de rayonnement \sigma quantifie le rendement de la conversion d’énergie mécanique de vibration en énergie acoustique. On le définit par la relation :
\displaystyle{ \boxed{ \sigma = \frac{\mathcal P_\text{ac}}{\rho_0 c S V_\text{eff}^2} }}
où le dénominateur correspond à la puissance acoustique de l’onde plane générée par un plan infini en vibration à la même vitesse, mesurée sur une surface égale à celle de la source. Or, pour la sphère pulsante, nous avons vu plus haut que :
\displaystyle{ \mathcal{P}_\text{ac} =\frac{\rho_0 \omega^2 S^2 V_0^2}{8\pi c} }
Ainsi, le facteur de rayonnement d’une sphère pulsante est :
\displaystyle{ \sigma = \frac{S \omega^2}{4\pi c^2} = R^2 k^2 }
L’efficatité du transfert de puissance varie donc comme le carré de la pulsation : elle sera faible dans les basses, comme cela a déjà été signalé.
Notons que la résistance acoustique peut s’écrire en fonction du facteur de rayonnement :
R_\text{R} = \rho_0 c S \sigma
Un fait important est à signaler ici. Une seule caractéristique du haut-parleur intervient dans la résistance acoustique et le facteur de rayonnement : son diamètre (et donc sa surface). En terme d’efficacité du transfert d’énergie mécanique de vibration vers l’énergie acoustique, le diamètre du haut-parleur est donc le seul facteur sur lequel on peut jouer.
Pour compenser une faible efficacité du transfert avec un petit haut-parleur, certains fabricants proposent d’augmenter la vitesse à laquelle vibre la membrane. Pour une même fréquence de vibration, cela consiste à augmenter l’excursion de la membrane du haut-parleur. Mais il faut bien voir que, dans la formule donnant la puissance acoustique, la surface est au carré et donc le diamètre à la puissance quatre : pour obtenir une puissance identique avec un haut-parleur de diamètre deux fois plus faible, il faudrait augmenter l’excursion maximale d’un facteur quatre. En regardant les caractéristiques des haut-parleurs “à grande excursion”, on se rend compte qu’ils sont loin de pouvoir rivaliser avec de grands haut-parleurs en terme de rendu de basse.
Puissance acoustique rayonnée
Nous pouvons maintenant retrouver l’expression de la puissance émise à partir des résultats précédents. La force de frottement fluide -R_\text{R}\underline{V} décrite par la résistance de rayonnement est responsable de l’émission d’ondes acoustiques.
La puissance acoustique s’obtient en prenant le produit scalaire de la force exercée par la source sur l’air avec la vitesse de l’air à l’interface, sa moyenne est donc :
\displaystyle{ \mathcal{P}_\text{ac} = \frac{1}{T} \, \int_0^T \Re(R_\text{R}\underline{V})\, \Re(\underline{V} )\text{d}t = R_\text{R}\frac{1}{T} \, \int_0^T \Re(\underline{V}\,\underline{V}^*) \text{d}t = R_\text{R} \frac{V_0^2}{2} }
Soit :
\boxed{\mathcal{P}_\text{ac} = R_\text{R}V_\text{eff}^2 }
En injectant l’expression de la résistance de rayonnement, on retrouve l’expression déjà calculée plus haut :
\displaystyle{ \mathcal{P}_\text{ac} = \frac{\rho_0 R^2 \omega^2 S}{c}\frac{V_0^2}{2} = \frac{\rho_0 }{8\pi c} \left( \omega Q_0\right)^2 }
Le dipôle acoustique
Description
On obtient un dipôle acoustique en plaçant à une faible distance L \ll \lambda l’un de l’autre deux monopôles vibrant en opposition de phase. On voit ici l’intérêt de la modélisation dans ce blog : lorsque la membrane d’un haut-parleur se déplace vers la droite, elle génère une surpression à droite et une dépression à gauche. Un haut-parleur non monté dans un caisson se comporte donc comme un dipôle.

La belle et simple symétrie sphérique du monopôle fait donc place à une symétrie cylindrique : les grandeurs physiques dépendront ici, en plus de la coordonnée r, de la coordonnée \theta.
Les deux sources en opposition de phase génèreront des interférences. En particulier, on peut déjà voir que, si l’observateur se place à \theta = \frac{\pi}{2}, il recevra au même instant les contributions opposées des deux monopôles : l’intensité sonore sera nulle.
Avant de rentrer dans les détails, voyons les conséquences dramatiques en terme de basses pour les haut-parleurs. Pour que la pression acoustique soit maximale, plaçons l’observateur sur l’axe y. Pour les grandes longueurs d’onde, la différence de marche entre les deux ondes sera faible : les ondes acoustiques générées par les deux monopôles s’annuleront presque en totalité. L’exemple ci-dessous indique le résultat de cette superposition pour une onde de fréquence f = 50 \,\text{Hz} et une distance L = 5 \, \text{cm}. Les courbes en pointillé indique la pression qu’on observerait avec chacun des monopôles émettant seul, la courbe verte est le résultat de la superposition des ondes acoustiques.

La pression acoustique est divisée par 20 entre le monopôle est le dipôle dans cet exemple : le niveau sonore produit par le dipole est donc 20 \,\log 20 = 26 \text{dB} en deça de celui produit par un monopôle de même débit !
Pression acoustique
Nommons Q_+ = Q_0 \exp{(j \omega t)} et Q_- = -Q_0 \exp{(j \omega t)} les débits acoustiques des deux sources, opposés puisqu’elles vibrent en opposition de phase. La pression acoustique obtenue est bien sûr la somme des pressions acoustiques provenant de chacun des monopôles :
\displaystyle{ \underline{p} = \underline{p}_+ + \underline{p}_- = \frac{ j \omega \rho_0 Q_+}{4\pi} \cdot \frac{\exp{ \left[-j kr_+ \right] }}{r_+} + \frac{ j \omega \rho_0 Q_-}{4\pi} \cdot \frac{\exp{ \left[ - j kr_- \right] }}{r_-} }
\displaystyle{ \iff \underline{p} = \frac{ j \omega \rho_0 Q_0}{4\pi} \cdot \left( \frac{\exp{ \left[- jkr_+ \right] }}{r_+} - \frac{\exp{ \left[ -jkr_- \right] }}{r_-} \right) \exp{(j \omega t)} }
On a r_+ et r_- proches de r, effectuons donc un développement de Taylor du terme entre parenthèses :
\frac{\exp (- jkr_+ ) }{r_+} \approx \frac{\exp (- jkr) }{r} + (r_+ - r) \frac{ \partial}{ \partial r} \left( \frac{\exp{(-jkr_+)}}{r_+}\right)_{r_+=r}
\iff \frac{\exp (- jkr_+ ) }{r_+} \approx \frac{\exp (- jkr) }{r} + (r_+ - r) (-\frac{1}{r}-jk) \frac{\exp{(-jkr)}}{r}
On fait de même pour le terme contenant les r_-, et on obtient :
\frac{\exp{ \left[- jkr_+ \right] }}{r_+} - \frac{\exp{ \left[ -jkr_- \right] }}{r_-} \approx (r_+ - r_-) (-\frac{1}{r^2}-\frac{jk}{r}) \exp (-jkr)
Exprimons maintenant r_+ -r_- en s’appuyant sur le schéma ci-dessous et sur le bon vieux théorème de Pythagore.

En notant (x,\,y) les coordonnées cartésiennes du point Md’observation :
r_+^2 - r_-^2 = \left( x^2 + \left( y + \frac{L}{2}\right)^2\right) - \left( x^2 + \left( y - \frac{L}{2}\right)^2\right) = 2Ly = 2L r \cos \theta
Par ailleurs : r_+^2 - r_-^2 = (r_+ - r_-)(r_+ + r_-) \approx 2r(r_+ - r_-) d’où r_+ - r_- \approx L \cos \theta.
Il vient alors pour la pression acoustique :
\displaystyle{ \underline{p} = -\frac{ j \omega \rho_0 Q_0}{4\pi} \cdot L \cos \theta \left(\frac{1}{r^2}+\frac{jk}{r}\right) \exp (-jkr) \exp{(j \omega t)} }
Soit :
\displaystyle{\boxed{ \underline{p} = \frac{ k^2 \rho_0 c L Q_0}{4\pi r} \, \cos \theta \, \left(1 + \frac{1}{jkr}\right) \exp [j(\omega t - kr)] }}
Contrairement au rayonnement du monopôle, deux termes apparaissent ici : un terme en 1/r^2 dominant en champ proche (kr \gg 1), et un terme en 1/r dominant en champ lointain (kr \ll 1). La limite définissant le champ lointain dépend bien sûr de la fréquence. Mais, pour une distance typique d’écoute de 3m, à 40 Hz :
kr = \frac{\omega}{c}r = \frac{2 \pi f}{c}r = \frac{2 \pi \times 40}{343}\times 3 = 2,19 > 1
La contribution du champ proche sera donc faible pour les graves et totalement négligeable pour les aigus : nous sommes davantage intéressés par le champ lointain pour lequel
\displaystyle{ \underline{p}_\text{CL} = \frac{ k^2 \rho_0 c L Q_0}{4\pi r} \, \cos \theta \, \exp [j(\omega t - kr)] }
Vitesse acoustique
Nous partons comme d’habitude de l’équation d’Euler linéarisée :
\displaystyle{\rho_0 j \omega\cdot \vec{\underline{u}} = - \vec{\nabla}\underline{p} }
avec en coordonnées cylindriques \vec{\nabla} = \frac{\partial}{\partial r} \vec{e}_r + \frac{1}{r}\frac{\partial}{\partial \theta} \vec{e}_\theta.
Il vient pour la coordonnée radiale :
\displaystyle{ \underline{u}_r = -\frac{1}{j \omega \rho_0} \frac{\partial}{\partial r}\underline{p} }
\displaystyle{ \iff \underline{u}_r = \frac{k^2 Q_0 L}{4\pi r} \cos \theta \left( 1 + \frac{2}{jkr} - \frac{2}{(kr)^2} \right) \exp \left[j(\omega t - kr)\right] }
La coordonnée suivant \theta est quant à elle :
\displaystyle{ \underline{u}_\theta = -\frac{1}{j \omega r \rho_0} \frac{\partial}{\partial \theta}\underline{p} }\displaystyle{ \iff \underline{u}_\theta = \frac{j k Q_0 L}{4\pi r^2} \sin \theta \left( 1 + \frac{1}{ jkr} \right) \exp \left[j(\omega t - kr)\right] } .
Intensité sonore
Seule la coordonnée radiale de la vitesse acoustique est à prendre en compte dans le calcul, puisque l’intensité sonore correspond à la puissance traversant une surface unité orthogonale à la direction de propagation de l’onde. Tous calculs faits, on obtient :
\displaystyle{ I = \frac{1}{2} \Re (\underline{p}\,\underline{u}_r^*) = \frac{\rho_0}{2c^3} \left( \frac{\omega^2 L Q_0}{4\pi r} \right)^2 \cos^2 \theta }Le niveau sonore s’en déduit comme d’habitude :
L = 10 \, \log\left(\frac{I}{I_0}\right)
Le diagramme de rayonnement d’un dipôle acoustique est représenté ci-dessous:

Le dipôle est porté par l’axe vertical, comme sur les figures précédentes.
Le niveau sonore est représenté, les cercles concentriques donnent les niveaux à +18, -3, -18 et -36 dB.
Le niveau baisse de 3dB autour de 45° : l’intensité sonore est alors divisée par deux.
Puissance acoustique
On l’obtient par intégration de l’intensité sonore sur une sphère centrée sur l’origine, l’élément de surface en coordonnées sphériques étant : \text{d}S = \sin(\theta) r^2 \text{d}\theta \text{d}\phi :
\mathcal{P}_ \text{ac} = \int_0^{2\pi} \int_0^{\pi} I(r) \sin(\theta) r^2 \text{d}\theta \text{d}\phi
\iff \mathcal{P}_ \text{ac} = \frac{\rho_0c}{16 \pi} \left(k^2LQ_0 \right)^2 \int_0^{\pi} \cos^2 (\theta) \sin(\theta) \text{d}\theta
\iff \boxed{ \mathcal{P}_ \text{ac} = \frac{\rho_0 c \omega^4}{24 \pi c^3} \left(LQ_0 \right)^2 }
Elle dépend, comme l’intensité acoustique, de la puissance 4 de la pulsation, alors que l’expression de la puissance acoustique pour le monopôle variait comme \omega^2.
La comparaison des deux expressions, à débits identiques, mène à :
\displaystyle{ \frac{\mathcal{P}_\text{monopôle}}{\mathcal{P}_\text{dipôle}} = \frac{3}{(kL)^2}}
Aux basses fréquences, ce rapport est grand : le dipôle est nettement moins efficace que le monopôle pour transférer son énergie à l’air. Ce résultat était déjà bien visible sur le diagramme de rayonnement.
Cela est dû, comme on l’a déjà dit, aux interférences destructives entre les deux ondes sonores. Pour un haut-parleur non monté, qui se comporte donc comme un dipôle, on parle de court-circuit acoustique pour décrire ce phénomène de réduction sensible de la puissance dans les graves : on voit bien la nécessité d’insérer le gaut-parleur dans un caisson pour supprimer l’onde arrière. Nous y reviendrons dans un article sur les enceintes closes.
Le piston circulaire bafflé
Description
Nous établirons ici un modèle du rayonnement d’une membrane de haut-parleur. Afin de se débarrasser de l’onde arrière et du court-circuit acoustique associé, la membrane sera considérée encastrée dans un plan (y,\, z) infini. Les fabricants d’enceintes diront que le haut-parleur est bafflé.
La membrane elle même sera modélisée comme un piston circulaire de rayon a et de surface S=\pi a^2 et sera à ce titre considérée comme plane et indéformable. De cette manière, tous les points de la membrane auront la même vitesse \vec{\underline{V}}(t) = V_0 \exp(j\omega t) et vibreront donc en phase.
Enfin, nous nous limiterons au calcul en champ lointain : on supposera kr \gg 1.
La situation étant symétrique par rotation autour de l’axe (Oy), il suffira de calculer les grandeurs acoustiques mesurées par des observateurs M situés dans le plan (y, \,z), dont les coordonnées polaires sont M(r, \,\theta).
Ce modèle est résumé sur la figure suivante :

Nous discuterons des limites de cette modélisation en fin de section.
Principe de Huygens-Fresnel
Nous avons ici à calculer les grandeurs acoustiques dues à une source étendue. La démarche pour attaquer un tel problème est la même qu’en optique pour l’étude de la diffraction. Le principe de Huygens-Fresnel stipule qu’une source étendue de surface S peut être décomposée en sources élémentaires sphériques de surfaces élémentaires \text{d}S. Les grandeurs acoustiques mesurées en M seront la somme des contributions des sources élémentaires.
Nous disposons déjà des sources élémentaires sphériques : il s’agit bien évidemment des monopôles acoustiques. Une subtilité s’introduit cependant ici. Les monopoles émettent sur la surface supposée parfaitement rigide du piston : l’onde émise vers le demi-espace y<0 est donc réfléchie vers l’avant de la membrane. Ainsi, la pression et la vitesse acoustiques mesurées à l’avant de la membrane seront deux fois plus importantes, tandis qu’elles seront nulles à l’arrière.
La formule de la pression acoustique établie en début d’article devient :
\displaystyle{ \underline{p} = \frac{ j \omega \rho_0 V_0\text{d}S}{2\pi} \cdot \frac{\exp{ \left[ j(\omega t - kr) \right] }}{r} }
Pression acoustique

Il s’agit donc d’intégrer au point d’observation M l’ensemble des contributions des sources élémentaires repérées par leurs coordonnées polaires (\mathcal{l}, \, \psi) dans le plan (x, \, z) :
\displaystyle{ \underline{p} = \frac{ j \omega \rho_0 V_0}{2\pi} \exp ( j\omega t) \int_0^{2\pi} \int_0^a \frac{\exp (- j k u)}{u} l\text{d}l \text{d}\psi }
Dans l’approximation du champ lointain M est à l’infini, \vec{u} et \vec{r} sont donc quasiment colinéaires. La figure ci-dessous représentant le plan contenant l’origine, M et \text{d}S permet de voir que u \approx r - l \cos \delta.

Par ailleurs, les relations de trigonométrie sphérique permettent d’écrire : \cos \delta = \cos \theta \cos \psi. L’expression de la pression devient :
\displaystyle{ \underline{p} = \frac{ j \omega \rho_0 V_0}{2\pi} \frac{\exp \left[ j(\omega t- kr)\right] }{r} \int_0^{2\pi} \int_0^a \exp ( j k l \cos \theta \cos \psi) l\text{d}l \text{d}\psi }\iff \displaystyle{ \underline{p} = \frac{ j \omega \rho_0 V_0}{2\pi} \frac{\exp \left[ j(\omega t- kr)\right] }{r} \int_0^a l \left( \int_0^{2\pi} \exp ( j k l \cos \theta \cos \psi) \text{d}\psi \right) \text{d}l }
Nous venons de tomber sur des fonctions de Bessel J_n régulièrement rencontrées en physique dans des problèmes à symétrie cylindrique, et dont les résultats sont connus :
\left\{ \begin{array}{ll} J_0(X) = \frac{1}{2\pi} \int_0^{2\pi} \exp (j X \cos \psi) \text{d}\psi \\ J_1(X) = \frac{1}{X} \int_0^X u \, J_0(u) \text{d}u \end{array} \right.
La double intégrale devient :
2\pi \int_0^a l J_0 \left(kl\cos\theta\right) \text{d}l
Puis, en posant u = kl\cos\theta :
\frac{2\pi}{k^2\cos^2\theta} \int_0^{ka\cos\theta} u \, J_0 (u)\, \text{d}u = \frac{2\pi a}{k\cos\theta}J_1 (ka\cos\theta) = S\cdot \frac{2J_1(ka\cos\theta)}{ka\cos\theta}
La pression acoustique au point M s’écrit donc :
\displaystyle{ \underline{p} = \frac{ j \omega \rho_0 Q_0}{2\pi} \frac{\exp \left[ j(\omega t- kr)\right]}{r} D(\theta) }
avec \displaystyle{ D(\theta) = \frac{2 J_1(ka \cos\theta)}{ka \cos \theta} } le facteur de directivité.
On retrouve l’expression de la pression acoustique pour un monopole émettant dans un demi-espace assorti dufacteur de directivité dépendant de \theta. Contrairement au dipôle, la directivité dépend ici de la fréquence de l’onde émise. L’allure du terme D(\theta) est donné sur la figure suivante :

Le haut-parleur reste peu directif aux faibles valeurs de ka, puis devient directif et des lobes secondaires apparaissent aux hautes fréquences.
Intensité sonore
La pression acoustique est le produit de la pression acoustique d’une onde sphérique par un nombre réel. On a donc :
\displaystyle{\boxed{ I = \frac{p_\text{eff}^2}{\rho_0 c} = \frac{ \rho}{2c} \left( \frac{\omega Q_0}{2\pi r} \right)^2 D(\theta)^2}}
Aux basses fréquences, l’émission est isotrope dans le demi-espace et D(\theta) \approx 1. On a alors pour un même débit :
I \approx 4 I_\text{monopôle}
Un facteur 2 provient d’une émission sur un demi-espace au lieu de l’espace entier, un autre s’explique par une résistance de rayonnement double (voir plus bas). Notons dès maintenant qu’il y aura une différence de 6dB dans le niveau sonore entre une émission monopolaire et une émission en piston bafflé, toute chose égale par ailleurs.
Le diagramme de rayonnement a l’allure suivante :

La pression est divisée par \sqrt{2} à u = 1,6 : l’intensité sonore est alors divisée par deux et le niveau sonore a chuté de 3 dB. Définissons la demi-ouverture du faisceau par l’angle \eta = \frac{\pi}{2} - \theta_{-3\text{dB}} :


- En deça de ka = 1,6, \theta_{-3\text{dB}} n’a pas d’existence et /eta = \frac{\pi}{2} : le haut parleur a une émission quasi-isotrope dans le demi-espace avant.
- Au-delà, on a \eta = \frac{\pi}{2} - \arccos \frac{1,6}{ka}.
- Il reste peu directif jusqu’à ka=3,9.
- Il devient très directif au-delà.
Impédance de rayonnement
Un long calcul aboutit au résultat suivant :
Z_\text{R} = \rho c S \left[ \sigma + j x_\text{R} \right]
avec le facteur de rayonnement \sigma = 1 - \frac{J_1 (2ka)}{ka} et x_\text{R} = \frac{S_1 (2ka)}{ka}
où J_1 est la fonction de Bessel d’orde 1 et S_1 celle de Struve. Le facteur de rayonnement est donc faible pour ka \ll 1 : le transfert d’énergie mécanique de la membrane en énergie acoustique se fait mal à basses fréquences, tant que la longueur d’onde de l’onde acoustique est supérieure à la dimension du piston. Le facteur de rayonnement tend ensuite vers 1 pour les hautes fréquences.
Ces deux fonctions sont représentées ci-dessous (les axes ont une échelle logarithmique) :

La résistance de rayonnement est donc R_\text{R} = \rho c S \sigma
La masse de rayonnement est quant à elle m_\text{R} = \rho c S x_\text{R} / \omega : elle varie avec la fréquence, contrairement à ce que nous avions vu pour la sphère pulsante. Elle est représentée ci-dessous (en g) pour un haut parleur de 14 cm de diamètre : elle est quasiment constante pour les basses fréquences puis chute autour de ka \approx 1 pour tendre vers zéro aux hautes fréquences.

Aux basses fréquences, un développement limité au premier ordre donne :
\displaystyle{ \left\{ \begin{array}{ll} \sigma \approx \frac{1}{2}(ka)^2 \\ x_\text{R} \approx \frac{8}{3\pi}ka \end{array} \right. \hspace{1cm} \text{d'où} \hspace{1cm} \left\{ \begin{array}{ll} R_\text{R} \approx 2\frac{\rho_0 S^2 \omega^2 }{4\pi c} \\ m_\text{R} \approx \frac{8}{3} \rho a^3 = \frac{16}{3\pi} \frac{\rho_0 S^{3/2}}{2\sqrt{\pi}} \end{array} \right.}
La résistance de rayonnement aux basses fréquence du piston bafflé est donc égale à celle d’un monopôle de même rayon émettant à la surface d’un plan parfaitement rigide. La masse de rayonnement est elle différente mais proche de celle d’un monopôle acoustique de même rayon émettant à la surface d’un plan parfaitement rigide (16/3\pi \approx 1,7).
Puissance acoustique rayonnée
Elle se calcule comme plus haut :
\displaystyle{\mathcal{P}_\text{ac} = R_\text{R} \, V_\text{eff}^2 = \rho c S \sigma \frac{V_0^2}{2} = \rho c S \left(1 - \frac{J_1 (2ka)}{ka}\right) \frac{V_0^2}{2} }
Soit :
\displaystyle{\boxed{ \mathcal{P}_\text{ac} = \frac{\rho c Q_0^2}{2\pi a^2} \left(1 - \frac{J_1(2ka)}{ka}\right) }}
Son allure, à débit constant, est donc l’allure de la courbe \sigma = f(ka). Mais nous devrons attendre le prochain article pour connaître la dynamique de la membrane et l’expression de son débit en fonction de la fréquence.
Aux basses fréquences, \sigma \approx \frac{1}{2} \left( ka \right)^2, la puissance rayonnée s’écrit alors :
\displaystyle{ \mathcal{P}_\text{ac} \approx \frac{\rho}{4\pi c} \left( \omega Q_0\right)^2=2\mathcal{P}_\text{monopole}}
Ainsi, d’une fait d’une résistance de rayonnement double, la puissance émise aux basses fréquences par un piston bafflé est double de celle émise par un monopôle de même débit.
Limites du modèle
Ces calculs sont valables dans l’approximation d’un piston circulaire plan, parfaitement rigide et encastré dans un plan infini.
- La forme conique des membranes usuelles de haut-parleur n’est pas prise en compte ici. La conséquence pour une membrane rigide est que l’onde émise par la périphérie est en avance de phase par rapport à celle émise au centre.
- La membrane n’est très rigide qu’aux basses fréquences. Lorsque la longueur d’onde de l’onde rayonnée devient petite par rapport aux dimensions de la membrane (\lambda \ll a ou f \gg c/a), d’autres modes de vibration de la membrane sont excités. On parle alors de fractionnement de la membrane : différentes zones vibrent avec différentes phases. Les ondes émises interfèrent et créent des accidents sur la courbe de réponse du haut-parleur.
- L’approximation du plan infini n’est strictement valable que pour des longueurs d’onde très petites par rapport à la taille L du baffle : \lambda \ll L ou f \gg c/L.
Conclusion
Nous avons vu dans cet article les différents modèles de sources sonores qui permettent d’expliquer le rayonnement de la membrane d’un haut parleur.
Le modèle du dipôle a montré qu’il était nécessaire d’enfermer le haut-parleur dans un caisson pour supprimer l’onde arrière et éviter le court-circuit acoustique responsable d’une perte de puissance importante, principalement aux basses fréquences.
Le modèle simple de la sphère pulsante est une bonne approximation du comportement d’une enceinte aux basses fréquences.
Pour les fréquences plus élevées, le modèle plus complet du piston bafflé doit être privilégié.
Aux très hautes fréquences, la membrane fractionne et aucun modèle simple ne peut rendre compte de son comportement exact.
Ces différentes domaines sont récapitulés sur la figure ci-dessous :

Nous sommes dorénavant outillés pour s’intéresser dans le prochain article au haut-parleur électrodynamique !
Sources
Optique – José-Philippe Pérez
Le cours d’acoustique de ECAN Lyon
Rayonnement acoustique – UPMC – Institut Jean Le Rond d’Alembert
Haut-parleurs et enceintes acoustiques : Théorie et pratique – Francis BROUCHIER

